Low-Frequency Loudspeakers Cancellation – Black Hole Sum
By Dale Shirk
At the Loudspeaker Arrays Workshop, Kurt Graffy demonstrated the cancellation that occurs between two low-frequency loudspeakers when one is reverse polarity. The question came up, “Where does the energy go?”
Some interesting discussions ensued. Kurt coined the phrase “black hole sum” to describe the effect. Dale Shirk offered some insights to the listserv regarding the “black hole sum.”
 A question came up regarding out-of-polarity drivers operating near each other and what happens to the energy that seems to disappear as they cancel each other. Conservation of Energy requires that all energy in the system must be accounted for.
A question came up regarding out-of-polarity drivers operating near each other and what happens to the energy that seems to disappear as they cancel each other. Conservation of Energy requires that all energy in the system must be accounted for.
I was busy spouting off a theory, but it turns out I was wrong. Well sort of. I had the right idea, but the details were backwards. The heart of the issue is the acoustic impedance the cone sees. Here is the amazing, math-free solution. To understand this we need some background on current drive and voltage drive.
Constant Voltage Systems
Most of the electrical items we use everyday operate from a constant voltage source, whether it’s AC, DC, audio or whatever. That is, the source’s output impedance is much lower than the load impedance. The source voltage remains more or less constant and the load impedance determines how much current will flow. Understand, in some cases such as audio, the source can send more or less voltage as it desires at the time, but the voltage it sends is not affected in any significant way by the presence or absence of the load. Since power is voltage times current, for a given voltage drive the load determines how much current is drawn and how much power is delivered. Lower load impedance means more current and more power. An open circuit is fine, but a short could be bad news, as the current will need to be limited.
Constant Current Systems
While every EE should be quite familiar with the concept, few if any common electrical interfaces use constant current operation. In this case the source’s output impedance is much higher than the load impedance. The source attempts to make the desired current flow by providing whatever voltage is necessary. The load impedance determines how high the voltage has to go in order to reach that current. Higher load impedance means more voltage is required, and more power is delivered. Read that again. It’s counter-intuitive. Higher load impedance means more power delivered. A short circuit is fine, the current flows but no voltage is developed, and no power delivered. However an open circuit is bad news, as the voltage will need to be limited.
Matched Systems
Brief aside, matched source and load impedances mean that an equal amount of power is dispersed in the source and in the load, and the maximum possible power (50%) is transferred.
Easy or Hard
Impedance means to impede the flow of current. Our line inputs have a high impedance and are very difficult to drive much current into. Indeed we don’t want to. But we’ve fallen into the habit of thinking that a high impedance input is “easy” to drive with our voltage sources. Thus we think of high impedance as “easy” and low impedance as “hard”. In truth, easy and hard are relative to what the source wants. A dead short of zero impedance is the easiest load for a current source to drive, as it need not develop voltage and deliver power, while a higher load impedance will require more voltage and power.
Mechanical Impedances
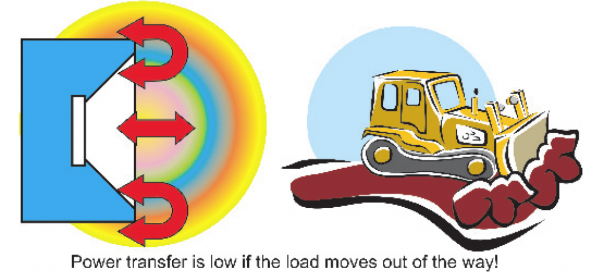
Those of us used to everyday electrical items have a strong bias towards the voltage source view of things and struggle a bit to grasp current source concepts. In the mechanical world current sourcing is more common than in electricity. That’s why electrical to mechanical analogies sometimes seem backwards to us. Remember, voltage is analogous to pressure and current is analogous to rate of flow. A bulldozer is a current (flow) source. It moves at a constant speed, but only develops pressure (voltage) on the blade when an impedance, a pile of dirt, is encountered. No dirt, zero impedance. Big rocks, high impedance.
Loudspeaker-to-Air Interface
So how does this relate to loudspeakers? The loudspeaker to air interface operates, like that bulldozer, in a constant current mode. The cone moves pretty much where the electromagnetic motor tells it to, with little regard for what air might be in the way. The air must move, and a current (flow) is created. The air component is only a small fraction of the equation dictating the loudspeaker’s behavior. Therefore the air only receives a small fraction of the power delivered by the amplifier and we get single digit efficiency numbers.
Confining ourselves to wavelengths much larger than the (direct-radiating) cone, we can see that the air that gets pushed by the cone can escape in every direction rather easily and little pressure is required to reach the flow dictated by the cone. There is a low impedance load, as little pressure (voltage) is required to achieve the flow (current).
However if we mount that cone onto the throat of a well designed horn, the cone gets asked to work a little harder and deliver more pressure to create the same flow. That’s because the air is confined and can’t get away. More pressure is required to achieve the desired flow, so there is a higher acoustic impedance. More power is delivered. An ideal horn will operate as a matched impedance circuit and deliver about 50% efficiency. Since the loudspeaker driver is a sort of impedance transformer this increased acoustic impedance will be reflected back to the source side and raise the electrical impedance seen by the amplifier. This is why an 8 Ohm horn loudspeaker may contain a 4 Ohm (free air) driver.
Back to the Question
So, back to the original question of two out-of-polarity drivers looking at each other. What is the pressure required to move the air (create the current) when, just as the cone is ready to shove, something else yanks the air away? No pressure is required of course. Flow without pressure, like current without voltage means zero impedance. Zero impedance means zero power delivered. Now if the driver, being a type of transformer, reflects this change from low impedance to no impedance, back to the source, the driver’s electrical impedance should actually decrease under these conditions.
This is where I got it wrong before I thought it through more carefully. I guessed the electrical impedance would go up so that less power would be drawn from the amp. Ironically additional power is drawn and it becomes heat in the voice coil.
If you attempt to measure these effects, two warnings: First the change in loading will change the tuning of reflex boxes and move the impedance spike by 10% or more. The skirts of this spike can look like the impedance change you’re seeking, but they’re not. Second, the effect you are looking for is very small, as in single digit percentages, not coincidentally similar to the efficiency of a direct radiator loudspeaker.
If you’ve read this far you should be impressed again, as I was, by how much of our amplifiers’ power heats voice coils and how little of it comes out the front of the box as sound. ds