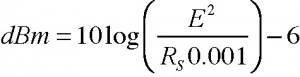dBm, dBW, dBV or dBu?
by Pat Brown
How should the output level of an audio device be specified – dBm, dBW, dBV or dBu??
A recent SynAudCon Forum thread posed an interesting question. How should the output level of an audio device be specified? It is ironic that given the advancements of audio technology over the last half-century that this is still a controversial topic.
All would agree that the rating should be in decibels. From a more basic perspective, the real question is whether I want to know the output power of a device or the output voltage. Then the choices are dBV, dBu for voltage and dBW or dBm for power.
Some Indisputable Facts
1. The universal interfacing method for analog audio optimizes the voltage transfer between two components. This means that a low source impedance drives a much higher load impedance. I can find no examples to the contrary in modern audio products. The typical source/load impedance mismatch is at least 1:10 but often 1:1000 or higher.
2. This means that the output voltage of an analog audio component does not change when it is connected to a high impedance load. For this reason, it is often referred to as a voltage source, and a voltmeter is sufficient for determining the output signal magnitude. Given this convention, the audio practitioner can generally connect an output to an input with no knowledge of the source or load impedance. This greatly simplifies the task of interfacing audio devices and makes interfaces more “plug and play.”
3. The input of an analog audio component has a voltage limit, established by its designer. Apply too much voltage and the signal is clipped. Apply too little voltage and the signal-to-noise ratio may be poor. This is the reason why we care about signal levels anyway. I’d like to be able to determine from specification sheets whether a given component will over drive or under drive another.
So, a modern analog audio interface is all about the voltage component of the audio signal. The current flow will be dependent on the load impedance, and it can only be adjusted by varying the voltage – which is exactly what a level (volume) control does. The current flow could also be changed by varying the load impedance, but that is a static value that is not user-adjustable. As long as the source has more current available than will be drawn by the load, all is good. This is exactly the same reason that we rarely think about how much current a household appliance draws when it is plugged into an electrical outlet. Unless the circuit is already powering other devices, or the device we are plugging in is a current hog (i.e. arc welder), there is little danger of drawing too much current and tripping the circuit breaker.
The voltage transfer optimized interface, whether in a household electrical circuit or an audio interface, makes using technology simpler. Simple is good.
So What About Power?
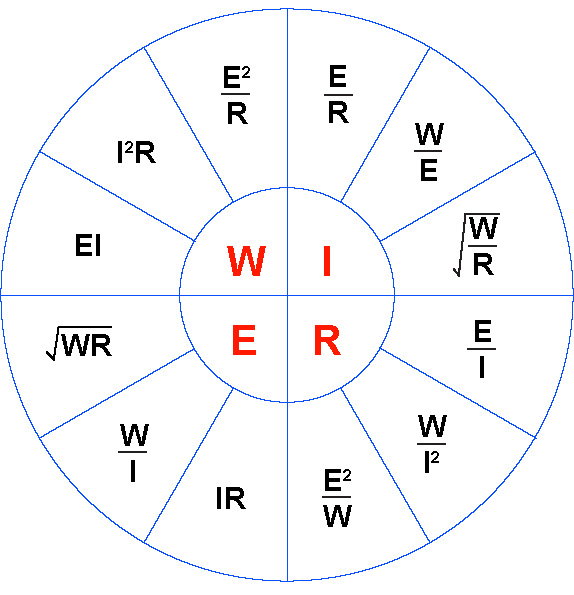
The classic “Ohm’s Law Wheel” also includes the power equations, which are not technically part of Ohm’s Law.
where
W is power in watts
E is electro-motive force in volts
I is current in amperes
R is resistance in ohms
Figure 1 – Ohm’s Law for DC circuits, including the power equations
This version is for DC circuits, where R is resistance in ohms. Ohm’s Law for AC circuits (which includes all audio signals) substitutes the impedance Z for the resistance R. Fortunately most impedances in audio interfaces are primarily resistive, or are treated as such for general design calculations. This allows us to stick with the simple versions. Simple is good.
When there is a danger of running out of current, we may need to think about whether or not the source can produce the signal voltage along with the amount of current demanded by the load. The most common example is a power amplifier driving a loudspeaker load. While the amplifier is interfaces as a voltage source, the current demand can exceed what is available, leading to “current limiting” which is a form of distortion. This is why amplifiers have a “minimum rated impedance” that they can safely drive.
Should My Mixer be Rated in dBm?
That’s fine, so long as the source impedance is specified. I can then use the power equation to determine the source voltage. It’s extra work and a good mental exercise, but ultimately I still get the output voltage. If the output level is given in dBm without a specified source impedance, the rating is useless. Why? Because there is no way to come up with the voltage. For example, 30 dBm is 1 watt of power. Here are a few examples of a voltage * current product that equals one watt.
1 W = 0.001 V * 1000 A
1 W = 0.01 V * 100 A
1 W = 0.1 V * 10 A
1 W = 1 V * 1 A
1 W = 10 V * 0.1 A
1 W = 100 V * 0.01 A
Just knowing the power is not enough to yield the voltage, and the voltage is what I need to know. Power ratings by themselves are seldom useful. Expressing them in dBm doesn’t change that. When a dBm rating is accompanied by the source impedance, we can use the Ohm’s Law wheel to solve for any quantity needed.
Does a dBm rating, which is a power rating expressed as a level, indicate how the device will perform under a load? Maybe. It depends on how it was measured. It is generally calculated from the open circuit voltage and source impedance using this equation.
It yields the power that should be available if the source voltage predictably drops by one-half in an impedance matched interface. But since it is not actually measured into the matched impedance, it is not a guarantee of performance. If the source device were terminated (impedance matched) and the voltage measured, then the dBm rating would indeed show how the device would perform under a load. Another way to express the “under load” performance is as follows.
Output Level: 20 dBV (600 ohm minimum load)
This tells me that the voltage will be independent of the load impedance, unless it falls below 600 ohms. If someone loads a modern device with a load impedance less than 600 ohms, they deserve for it to not work.
Some erroneously assume that the dBu and the dBm are the same thing, so 24 dBu equals 24 dBm. This is not even remotely true. The dBu and the dBm are numerically the same if the source impedance of the device is 600 ohms (rarely true in sound reinforcement), and the device is unloaded (driving a very high impedance relative to its source impedance).
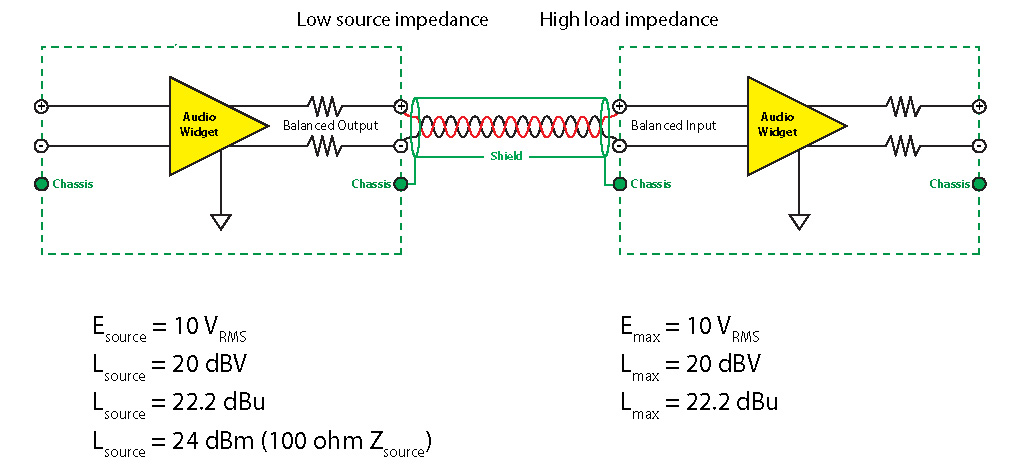 Figure 2 – A good marriage between a source and a load, with relevant levels of each specified (click to enlarge).
Figure 2 – A good marriage between a source and a load, with relevant levels of each specified (click to enlarge).
Amplifiers Need Power Ratings, Right?
It is logical to think that a “power amp” needs a power rating. Ironically, it does not. Amplifiers have been specified based on voltage for decades. The “70.7 system” is a prime example. This voltage, along with the rated minimum load impedance is all one needs to deploy the amplifier. Alternately, the line voltage (70.7 VRMS) along with a power rating accomplishes the same thing, allowing the system designer or installer to calculate the minimum load impedance to ensure that the amplifier is not overloaded. Just knowing the power rating is not enough. A “100 watt” amplifier could mean
100 V * 1 A
1 V * 100 A
28 V * 3.5 A
Amplifiers designed for “voice coil” connection are no different. They are typically rated in watts into a resistive load, such as 8 ohms, 4 ohms, etc. If you want the voltage, you will have to calculate it using the power equation. But, if these amplifiers were given a voltage rating and minimum load impedance, like the “70.7 volt system” you would have exactly the information needed to deploy the amplifier. Even for a power amplifier, a wattage rating by itself is useless. We need enough information to put the power equation to work, which means any two of power, voltage, current or impedance.
Back to the Original Question
dBV and dBu are voltages expressed as levels. If the voltage is the parameter of interest, then dBV or dBu should be used. They are calculated using these formulas. Professional audio tends to prefer dBu, while consumer audio tends to prefer dBV. The formulas are as follows:
dBV = 20 log E
dBu = 20 log E/0.775
The utility is obvious. If my source can output +30 dBV and my load (input) can only accept +20 dBV before clipping, I must either turn the source down by 10 dB or install a -10 dB in-line attenuator. If my source level is -40 dBu and I wish to drive the mixer to +4 dBu, I need 44 dB of gain from the mixer’s input stage. Anytime gains or losses are of interest, which is about all of the time, the dB is extremely useful. If fact, why would we use anything else? The better voltmeters allow the measured voltage to be displayed as voltage, dBu ordBV and even dBm with a user-specified impedance.
DBW and dBm are wattages expressed as levels. If power is the quantity of interest, then dBm or dBW should be used. Here are the conversion formulas.
dBW = 10 log W
dBm = 10 log W/0.001
Conclusion
There’s more than one way to do about anything in audio. Specifying input or output levels is no exception. Rather than engage in the ongoing debates regarding right or wrong, just train yourself to use any of them, and to convert between them. I have my favorites, and you’ll have yours. But we can get the job done with any of them, and that’s what it’s all about. pb