Solving Engineering Problems | Trial-And-Error vs Math
By Bruce Bartlett 5-28-2018
The job of an engineer is to solve problems. Bruce Bartlett looks at two approaches to solving engineering problems – math vs trial-and-error.
As engineers, our task is to create solutions that solve problems. For example, design a sound system to minimize feedback or determine the sonic effect of an object placed next to a microphone.
Two problem-solving methods are trial-and-error and prediction using mathematics. With trial-and-error, you come up with a solution intuitively, try it out, and see what happens. It’s cut-and-try. It’s repeated varied attempts that you continue until you reach success. Alternatively, you predict a result using math equations, or using the known properties of an object. Then test your prediction with real-world measurements.
Trial-and-error doesn’t necessarily produce the best result, but it’s often good enough.
Photo 1: Solving Engineering Problems – Trial and Error Method
The physical properties and geometry of objects create the mathematical laws of physics. Sometimes, using trial-and-error methods we can let the laws of physics do the heavy lifting of complex math to produce a desired result. In other words, reality produces the same result that you would get with the correct math equations.
With trial and error, you do an experiment – change one variable in a system – and measure the results. Instead of using math to calculate and predict the results of that experiment, you let nature’s laws “calculate” or form the result as an analog computer would. Nature “does the math” perfectly when it produces a result of an experiment.
Sometimes nature is too complex mathematically for us to predict a result using our limited knowledge of what’s going on physically. For example, how does a small object or an open slit next to a mic capsule affect its frequency response? If you tried to predict it with math, you’d need to know about fluid dynamics, geometry, the exact shape of the bump or slit, resonance, effect of obstacles of various shapes on sound waves (diffraction), etc.
But if you just create an object or slit, and measure the result (the delta or change in frequency response), nature “worked out the math” for you, effortlessly and precisely. Sometimes, cut-and-try gives usable results much faster than calculations.
If you want, you could come up with equations and try to match them to the data that nature has already “calculated” for you.
An Empirical Approach
Here’s an example. Suppose you have a P.A. system, and you want to create the loudest sound without feedback. You place a mic and speaker in certain locations relative to the sound source. You turn up the volume until feedback just starts. Then change one variable. For example, increase the distance of the loudspeaker from the mic. If the feedback stops, you can turn up the volume a little until feedback just starts again. From what you just learned, you can write an equation: Loudness before feedback is proportional to the distance from speaker to mic.
SPL ∝ D1*X
where
SPL is loudness,
X is an unknown constant or variable, and
D1 is the distance from speaker to mic.
Then you change another variable and see what happens. You move the mic closer to the sound source. The loudness of the sound system increases without causing feedback. So you make another equation:
SPL ∝ X/Ds
where
L is loudness,
X is an unknown constant or variable, and
Ds is the distance from mic to source.
Combining those two equations, you get SPL ∝ D1*X/Ds. You are starting to make an equation that predicts gain-before-feedback.
Now you change another variable. You move the loudspeaker closer to the listener. The sound system gets louder at the listener without causing feedback. As a mathematical expression, you might say
SPL ∝ X/D2
where
SPL is loudness,
X is an unknown constant or variable, and
D2 is the distance from loudspeaker to listener.
Combining those three equations, you get
SPL ∝ D1*X/(Ds*D2)
Our equation to predict gain-before-feedback is becoming more complete. It tells you this: if you want to increase loudness, then increase the distance from the speaker to the mic, decrease the mic-to-source distance, and decrease the speaker-to-listener distance. In other words, place the speaker far from the mic, place the mic close to the source, and place the speaker close to the audience.
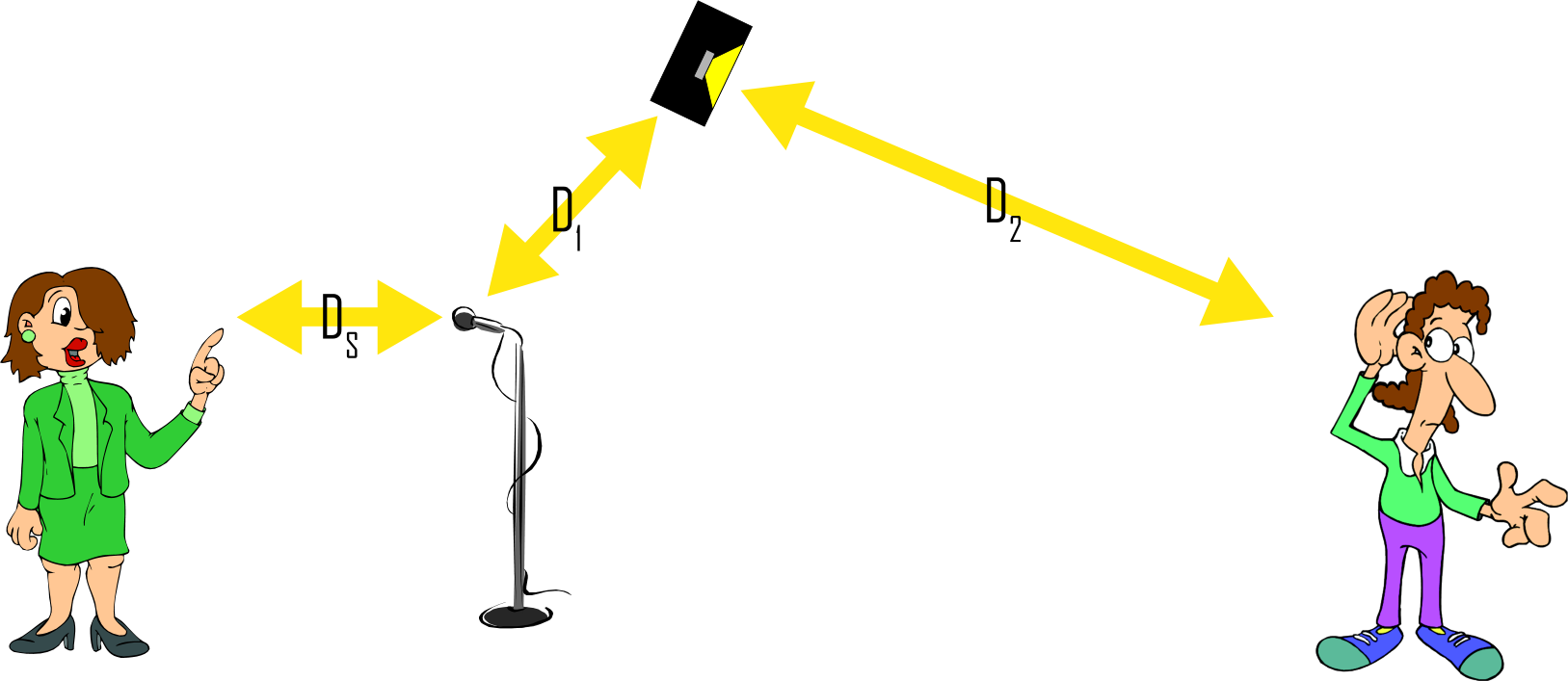
Photo 2: Solving Engineering Problems – Using Math
X in that equation could be other variables such as as the frequency response and sensitivity of the mic in the direction of the speaker, the response and sensitivity of the speaker in the direction of the mic, the microphone polar pattern, the speaker polar pattern, the liveness of the room, the loudness of the sound source, etc.
X could also be an equation itself. We could start with the inverse square law relating SPL to distance, and derive our feedback equation from there.
Reality doesn’t follow equations. It just responds to circumstances in the only way it can. Humans write equations that describe how reality deals with circumstances, and we call those equations “laws of physics.” A law says, X always occurs when Y conditions exist.
A Direct Engineering Solution
Sometimes calculations are more efficient than trial-and-error. Suppose you want to send a rocket around the moon and back to earth. You could launch several rockets of various sizes and thrust, and pick one that did the job. But that’s very expensive and slow. Instead, you can work out the math first, design a rocket and set the thrust duration and vector to match that math, then launch the rocket and hope for the best. If your math modeled reality accurately, you can launch a rocket designed around that math and it will actually go around the moon and back.
In much of our engineering work, we combine the two methods to make educated guesses. Or we design a system using math, try it out in the real world, and adjust for the differences between theory and experience. Whatever works. :>) bb

Photo 3: Science doodles on paper with 3d fountain pen.
