CALCULATING Reverberation Time (RT)
Since the introduction of computerized acoustical analysis software, acousticians often build and run computer models to predict the reverberation time (RT). Yet there are still cases in which manual RT calculations are helpful.
We all know that Wallace Clement Sabine’s investigations into reverberation in rooms and his subsequent introduction of the Sabine equation for calculating Reverberation Time (RT) are commonly heralded as the birth of scientific acoustics. For many years, manual calculations using statistical geometric acoustics approaches such as the Sabine equation were the standard method of predicting the RT of a planned new or to-be-renovated acoustical space. Since the introduction of computerized acoustical analysis software such as EASE, CATT Acoustics, ODEON, and other programs, acousticians often build and run computer models to predict RT.
Yet there are still cases in which manual RT calculations are helpful. A spreadsheet analysis using the statistical approach can help us find a starting place for configuring acoustical absorption in a computer model, or it can help us estimate how to fine-tune the type and placement of absorption in order to achieve our target RT. For conference rooms, especially those supporting teleconferencing, spreadsheet analysis is often more expedient and faster than computer modeling.
Statistical Calculations for Predicting RT
The Sabine equation is:
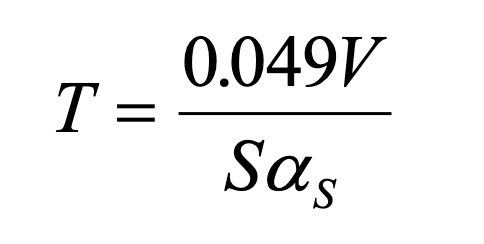
where V is the volume of the room in cubic feet,
S is the total boundary area (walls, ceiling, and floor),
and αS is the mean absorption coefficient as defined by Sabine
for measurements using the Imperial units, or
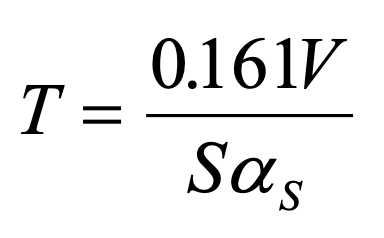
for SI units. (Although Sabine gave the constant for Imperial units as 0.05, in modern texts, the constant in the numerator is usually given as 0.049.)
As early as the 1932 publication of Vern Knudson’s Architectural Acoustics, a problem with Sabine’s approach was noted. In Appendix II of Knudsen’s book, R. F. Norris pointed out that Sabine assumed an absorption coefficient of unity for a perfect absorber such as an open window; whereas, that value used in the Sabine equation does not yield a prediction of zero RT. Obviously, if the absorption coefficient as usually described (decimal fraction of incident sound absorbed) were unity, all sound would be absorbed upon first striking the absorptive material, so there would be no reverberant sound, and hence, an RT of zero. Denoting Sabine’s absorption coefficient as a, and the “true absorption coefficient” as α (Greek lower-case alpha), Norris derived an equation based on the mean free path of a sound wave in a reverberant room, from which he defined the true absorption as:
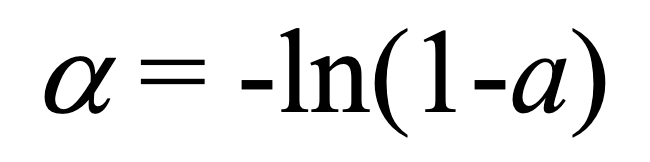
As you can see from Norris’s graph shown in Figure 1 below (Knudsen page 604), a Sabine absorption coefficient corresponds to a “true absorption coefficient”of 0.63.
![Figure 1: R. F. Noris plotted the Sabine absorption coefficient (vertical axis) gainst his "true absorption coefficient (horizontal axis). [Knudsen, op. cit.]](https://www.prosoundtraining.com/wp-content/uploads/2024/03/RT-Fig1-Norris-Lmudsen.bmp)
Figure 1: R. F. Noris plotted the Sabine absorption coefficient (vertical axis) gainst his “true absorption coefficient (horizontal axis). [Knudsen, op. cit.]
In the graph, he uses α for the Sabine coefficient, and Q for the “true coefficient”, differing from his nomenclature in the equations.
Carl F. Eyring noted, as had others, that Sabine’s formula worked better for live rooms (little absorption) than for dead rooms ( lots of absorption). In 1930, he published “Reverberation Time in ‘Dead’ Rooms”; J. Acoust. Soc. Am. 1, 217–241 (1930); https://doi.org/10.1121/1.1915175, in which he used the “method of images” and mean free path analysis to derive an RT equation identical to that of Norris:
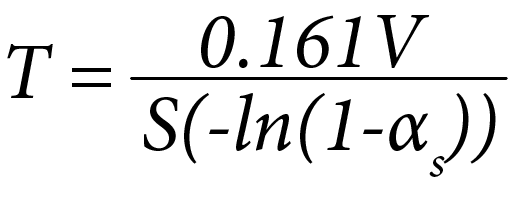
This expression is variously called the “Norris-Eyring equation or the “Eyring” equation. Some computerized acoustical modeling platforms, such as EASE and CATT Acoustic, automatically calculate a statistically-derived RT using both the Sabine and the Eyring methods. The RT’s Calculated using these methods are found to agree for live rooms, but Eyring gives a lower RT than Sabine for dead rooms, as indicated in Figure 2 below.
![Figure 2: With the constant (0.049 or 0.161), the volume, and the surface area factored out, and the only remaining variable being the expression for average absorption, Eyring and Sabine results differ mainly for dead rooms.[Eyring, op. cit.]](https://www.prosoundtraining.com/wp-content/uploads/2024/03/Eyring_graph.png)
Figure 2: With the constant (0.049 or 0.161), the volume, and the surface area factored out, and the only remaining variable being the expression for average absorption, Eyring and Sabine results differ mainly for dead rooms.[Eyring, op. cit.]
This is a good time to point out that all the statistical equations for RT are based on the assumptions of homogeneity (at any point in time, the reverberant sound level is the same at all points in the room), isotropy (reverberant sound is equally likely to arrive from any direction), and diffusivness (sound from any point can spread equally in all directions). In practice, this would mean that there is no focusing of sound, and the acoustical absorption is equally distributed on all surfaces in the room. In practice, these conditions are essentially never met.
In 1959, Dariel Fitzroy published “Reverberation Formula Which Seems to Be More Accurate with Nonuniform Distribution of Absorption”; JASA, 31, 7 (July, 1959), in which he introduced an empirically derived equation for calculating RT that took into account varying acoustical absorptivity in three orthogonal directions (x, y, and z):
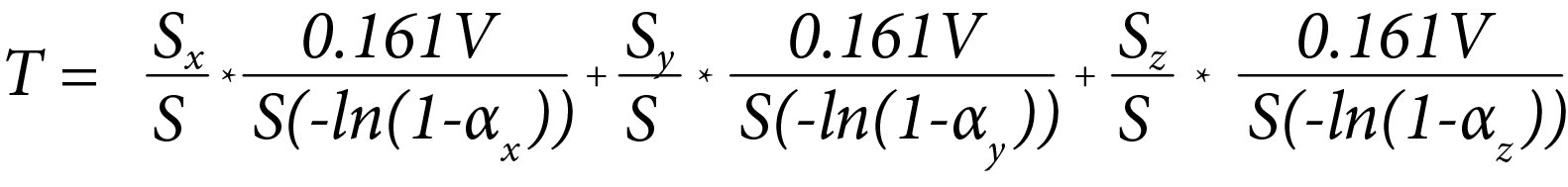Where Sx, Sy, and Sz correspond to the areas of absorption in planes perpendicular to the x, y, and z axes and αx, αy, and αz are the corresponding absorption coefficients.
The effectiveness of this formula overcomes the inaccuracies imposed by lack of isotropy and diffusiveness. Table A below shows that the Fitzroy equation yields results that often match RT measurements more closely than does Eyring.
![Table A: Fitzroy's "New Formula" predictions often match test results better than Eyring does. [Fitzroy op. cit.]](https://www.prosoundtraining.com/wp-content/uploads/2024/03/Fitz_Table.png)
Table A: Fitzroy’s “New Formula” predictions often match test results better than Eyring does. [Fitzroy op. cit.]
In February, 1980, W. B. Joyce published “Power series for the reverberation time”; JASA 67, 564-571. https://doi.org/10.1121/1.383922, in which he enumerates errors in the Eyring equation, and offers corrections. In his textbook Room Acoustics, Heinrich Kuttruff offers additional corrections to Eyring that are said to improve prediction accuracy depending upon the room shape.
In 1988, Higini Arau-Puchades published “An Improved Reverberation Formula in Akustica (65, 163-180), in which he examined a further development of Fitzroy’s model. His RT equation is given as:
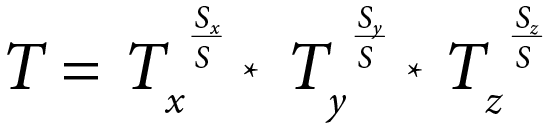
where Tx, Tx, and Tz are the RTs calculated using the Eyring equation with the total volume, the areas perpendicular to the x, y, and z axes, respectively, and the mean absorption coefficients αx, αy, and αz, of those three areas,
Sx, Sx, and Sz are the corresponding areas,
And S is the total wall, ceiling, and floor area of the room.
Arau-Puchades includes results from a theoretical/experimental comparison of RT predictions and measurements of a 4.5m×2.73m×2.4m rectangular room performed by M. I. Mehta and K. A Mulholland and reported in “Éffect of Non-Uniform Distribution of Absorption on Reverberation Time” [J. Sound Vib. 46 (1976) 209]. Five different layouts of absorptive treatment (absorption coefficient of 0.86) were used. The results are given in Table B below.
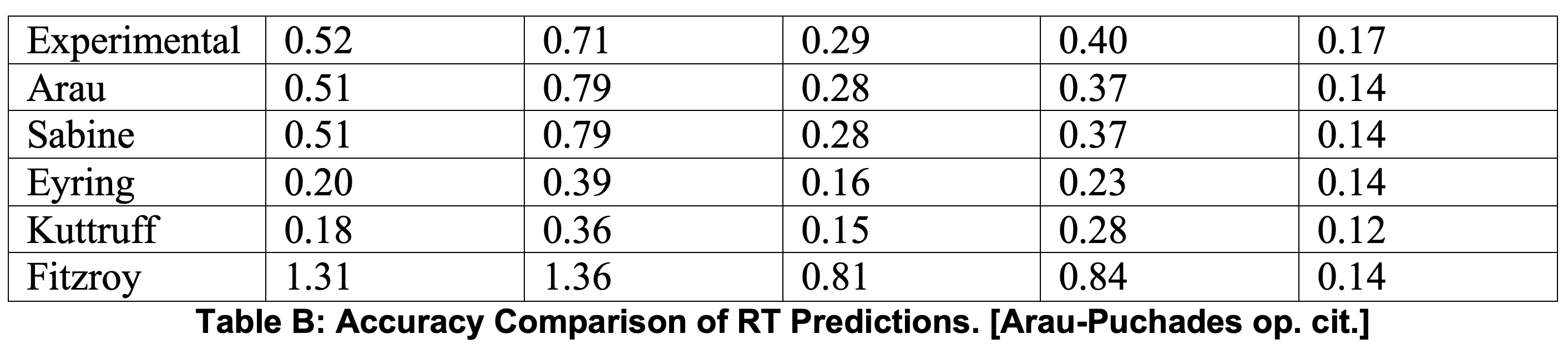
For this fairly small room, the Arau-Puchades equation clearly gives RT predictions aligning more closely with measured values.
The measured and predicted RTs shown in Tables A and B are mid-frequency values ( typically 500 Hz). An appropriate mid-frequency RT does not ensure good acoustics for either speech or music. [Shameless self-promotion: see my book Acoustics for Performance and Worship (https://www.elektor.com/products/acoustics-in-performance ) for further discussion.] For this reason, manufacturers of acoustically absorptive materials typically provide 1/3-octave band absorption coefficient test results from accredited laboratories. Figure 3 shows the test results for Armstrong Optima Open Plan 1” fiberglass ceiling tiles in a E400 mounting (tiles in a grid 400mm below a hard ceiling).
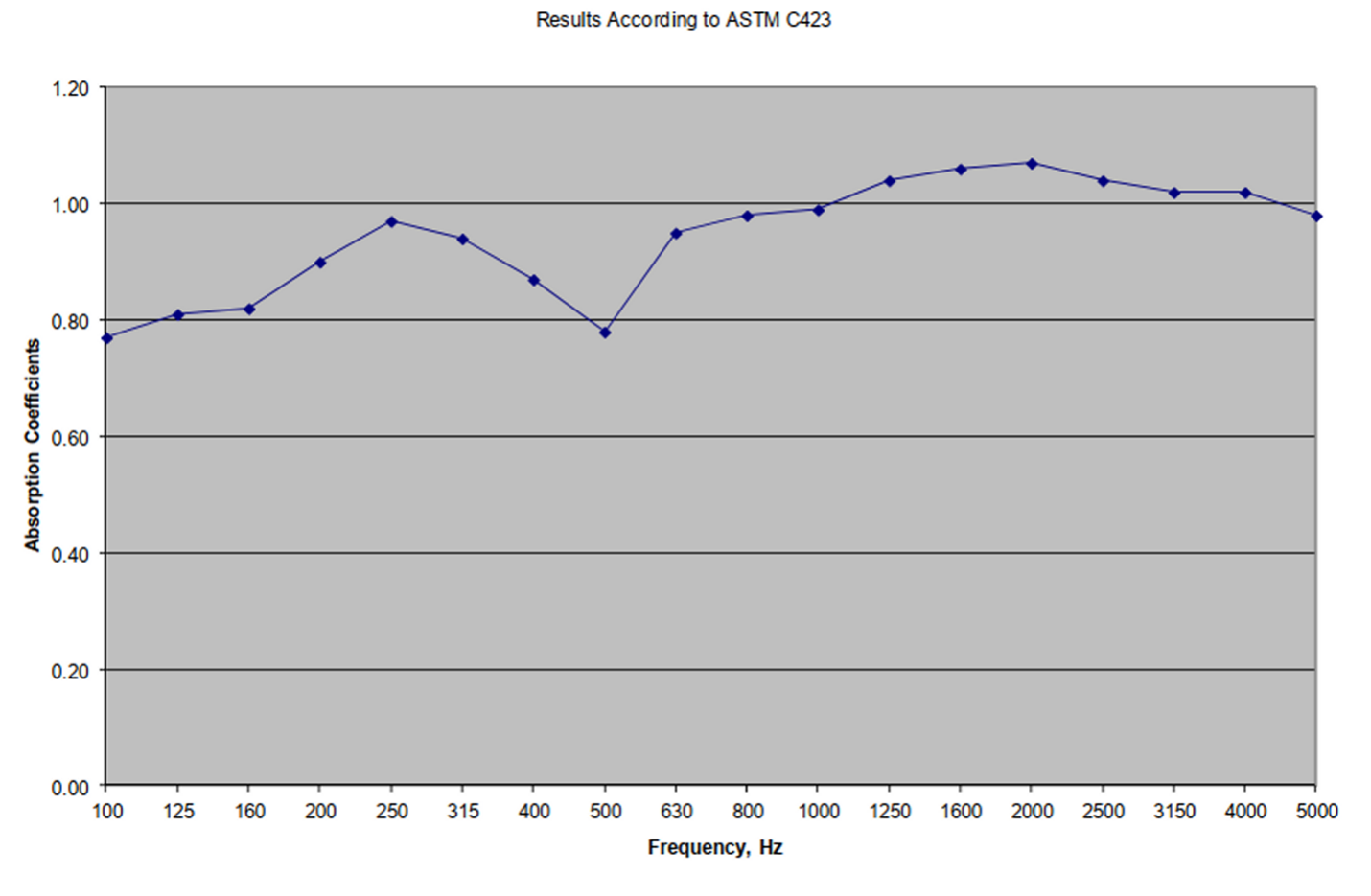
Figure 3: The absorption coefficient of 1″ fiberglass ceiling tiles cannot be described by a single number.
Even using the best equation to predict RT in full or 1/3 octave bands does not guarantee precise results, because of edge effect and other wave phenomena discussed in my previous blogs. A June 2023 update on the discussions in progress regarding this topic can be viewed at https://www.youtube.com/watch?v=q36dC4SqqJc. rh