Sizing an Amplifier Based On Target Voltage

by Pat Brown

Pat gives to two perspectives when sizing an amplifier – power and voltage.

A loudspeaker “power handling” test determines the maximum RMS voltage that can be applied to a loudspeaker before the onset of excessive power compression. The amplifier output voltage can be monitored in the field with a True RMS voltmeter to assure compliance.

This voltage-dependence must influence the selection of an appropriate amplifier for a loudspeaker in terms of its power rating and SPL production.

Let’s consider two loudspeakers. Both have a voltage limit of 40 Vrms as determined from a power handling test. The impedance of Unit A is rated at 6 ohms. Unit B is rated at 20 ohms. The objective is to select an amplifier for each unit that will provide the loudspeaker’s maximum allowable voltage, to the end of producing the maximum possible SPL.

I will approach the problem from two perspectives, that of power, and that of voltage.

Power

From the power equation, unit A can handle 267 W continuous.

W = 40²/6 = 267 W

Also from the power equation, unit B can handle 80 W continous.

W = 40²/20 = 80 W

If amplifier selection and SPL prediction are based on the power, Unit A and Unit B have very different needs.

Voltage

The figure shows a plot of an amplifier’s output voltage vs. impedance. For all real-world loads (average impedance > 4 ohms) the amplifier’s output voltage is independent of the loudspeaker’s impedance.

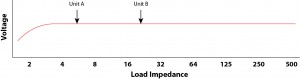
Click to enlarge.

A modern amplifier is a voltage source. The output current (and power) will rise or fall as determined by the impedance of the loudspeaker, but the output voltage is independent of the loudspeaker’s impedance unless it becomes too low. Unit A will draw more current from a given amplifier than Unit B, but both will have the same voltage developed across them.

So what we really need is an amplifier that can produce 40 Vrms into either loudspeaker.

The Amplifier

To size an amplifier based on voltage, we must select a reference impedance that is on the flat portion of the curve, for which we have a power rating for the amplifier. 8 ohms is a logical candidate.

If both Unit A and Unit B are assumed to be 8 ohms, then the required amplifier size to deliver 40 Vrms can be easily determined from the power equation

W = 40²/8 = 200 W

A “200 W into 8 ohm” amplifier will deliver 40 Vrms to either loudspeaker. Both loudspeakers will require exactly the same amplifier, because both have the same RMS voltage limit.

If the amplifier selection criteria were based on power, the amplifier for Unit A would have been over-sized and the amplifier for Unit B under-sized. If SPL predictions were based on power, the SPL would have been over-stated for Unit A and under-stated for Unit B.

To size an amplifier based on the required voltage, the loudspeaker’s impedance should just be normalized to 8 ohms.

Smart Amplifiers

Some modern amplifiers are smart enough to reduce their output voltage when excessively loaded. The amplifier in Figure 2 has a “Load” LED that is “off” when the load impedance is > 16 ohms, “on” when it is between 2 ohms and 16 ohms, and “flashing” when less than two ohms. This lets me know at a glance where I am on the amplifier’s voltage vs. impedance curve, and serves as a reminder to not overload the amplifier.

In closing, remember that in reality the amplifier must be over-sized to allow for signal peaks above the average voltage of the signal. If we really do intend to deliver 40 Vrms to either of these loudspeakers, then a much larger amplifier would be required.pb