Fine Points of Aiming One-box Line Arrays — II
by Richard Honeycutt
Fine Points of Aiming One-box Line Arrays – Richard Honeycutt looks at practical aiming considerations.
The directionality of any sound source changes with the distance from the source. Close to the source — in the “near field” — the directivity does not match the simple approximations we usually use to predict coverage; these approximations are valid only in the “far field”. In the near field, SPL drops off at a lower rate than the 6 dB per doubling of distance we see in the far field (assuming anechoic conditions). The transition from near-field to far-field behavior is frequency-dependent, and occurs at a distance given by r > or =8a2/λ, where r is the distance from the source, a is the width (for horizontal directivity considerations) or height (for vertical directivity) of the source, and λ is the wavelength. [Introduction to Electroacoustics and Audio Amplifier Design, by W. Marshall Leach, Jr., Kendall/Hunt Publishers, 1998, p. 37]. Beranek adds that r must be a minimum of 3 times the source diameter [Acoustics, McGraw-Hill, 1954, p. 100.]
Pat Brown gives more thorough discussion in http://www.synaudcon.com/site/author/pat-brown/far-field-criteria-for-loudspeaker-balloon-data/.
For a 15″ speaker, these conditions indicate the transition to far field is the greater of about 45″ (Beranek condition); or 23.3″ ( Leach equation at 100 Hz), 19.4′ ( Leach equation at 1 kHz), or 194′ ( Leach equation at 10 kHz). Pat’s article includes a convenient table to allow you to avoid calculations. Using the table, we see that for a 4′ one-box line array, the vertical directivity settles to far-field conditions at about 30′ for frequencies of 4.2 kHz and below.
Two types of one-box line arrays provide reduced effective dimensions for the source at higher frequencies. The Bessel array uses LC circuits to taper the response from full-range in the center to only low frequencies at the ends. Most steerable arrays perform the same sort of frequency tapering by internal digital filtering. This reduces the transition distance.
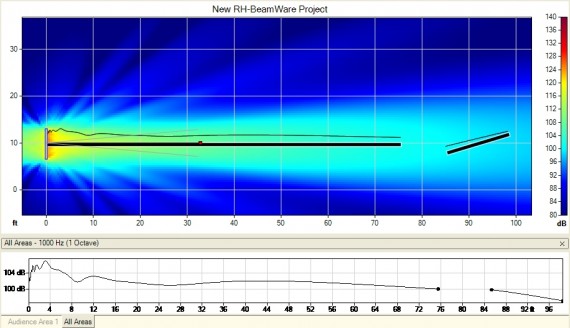
The bottom line is that you can’t count on actual devices matching the theoretical performance if the listeners are close to the line array. Or in somebody’s words (the experts disagree as to whose words): in theory, theory and practice should be the same, but in practice, they’re not. This fact shows up in the shape of the level graph for a Renkus-Heinz IC16 at 1 kHz (Figure 1), which does not smooth out until the distance reaches about 40′.
Figure 1: Renkus-Heinz IC-16 Single Beam at 1 kHz
Another fine point about line arrays that is not always appreciated is that the frequency response varies with distance from the array. This makes sense if you remember that the SPL variation with distance changes with frequency. Figures 2 and 3 illustrate this variation for an SLS LS-8695. (The vertical axis is marked in 5-dB increments; the horizontal axis, in 1/3-octave increments.)
Figure 2: SLS LS-8695 Frequency Response at 23′ on Axis
Figure 3: SLS LS8695 Frequency Response 48′ on Axis
In a closed room, this variation will be less noticeable than it looks, since the wide horizontal coverage of the line array ensures abundant sidewall reflections so that the reflections and reverberation even out some of the gaps that show in the direct field at great distances.
In Part III of this blog series, we’ll look at some unintended consequences of beam steering and at the interaction between choice of aiming and the architecture of the room. rh
Richard A. Honeycutt developed an interest in acoustics and electronics while in elementary school. He assisted with film projection, PA system operation, and audio recording throughout middle and high school. He has been an active holder of the First Class Commercial FCC Radiotelephone license since 1969, and graduated with a BS in Physics from Wake Forest University in 1970, after serving as Student Engineer and Student Station Manager at 50-kW WFDD-FM. His career includes writing engineering and maintenance documents for the Bell Telephone System, operating a loudspeaker manufacture company, teaching Electronics Engineering Technology at the college level, designing and installing audio and video systems, and consulting in acoustics and audio/video design. He earned his Ph.D. in Electroacoustics from the Union Institute in 2004. He is known worldwide as a writer on electronics, acoustics, and philosophy. His two most recent books are Acoustics in Performance and The State of Hollow-State Audio, both published by Elektor.