Why, What, and How to Test For Correct Speaker Aiming and Equalization Settings
by Richard Honeycutt
Commissioning a sound system is the last step of the installation process. This article will focus on testing for proper speaker aiming and EQ adjustment.
So you’ve finished the installation and are ready to sit back and enjoy the results of your labor! But then you realize that you haven’t reached the “enjoy” moment yet: there’s still testing to be done.
Many types of testing are involved in commissioning a sound system, but for now, we’ll focus on testing for proper speaker aiming and EQ adjustment. Naturally you took care in installing the speakers with the correct aim points, and thoughtfully pre-set the EQ (SP or graphic), but you’re not finished without thorough testing. Many contractors, and not a few consultants, not to mention system operators who do their own upgrades, settle for an LAR (looks about right) approach, figuring that any necessary tweaking will be done at the first sound check. I respectfully submit that this makes about as much sense as filling out your 1040 from memory and figuring that if you get audited, any errors will be found then.
When checking for correct speaker aiming, there is no substitute for walking the space while holding a portable RTA and observing the response variations. An alternative method is to use a portable digital recorder with a test-grade mic and make short measurements of pink noise at various locations. Thoroughly document which recorded segment corresponds to which position, then you can analyze later at your computer.
What you’re looking for is where, at the edges of the seating area, the HF response drops noticeably. In order to know what counts as “dropping”, you first need to note the response in the central part of the seating area. I often focus on the 10-kHz band for this test, because few people can tell the difference if a sound system cuts off at 12 kHz as opposed to 20 kHz, even if they can actually hear up to 20 kHz. (Also, many listeners in our world of iPads and snowmobiles cannot hear much, if at all, above 10 kHz.) The 10-kHz one-third octave covers from just below 8 kHz to just above 11 kHz. The
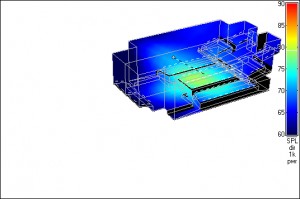
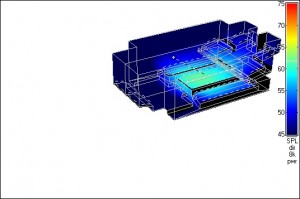
HF falloff happens at a different place from where the overall SPL drops noticeably, since virtually all directional speakers have wider coverage at lower frequencies than at higher frequencies. If you make this listening test using white noise rather than pink noise, since the higher frequencies are more prominent in white noise, your ears will help you quickly find the places that you need to measure. Just be careful with the levels when using white noise, since mid and tweeter drivers will not handle anywhere near as much power as woofers, and white noise is equal in energy per Hz; whereas, pink noise is equal in energy per octave. Figure 1 shows the CATT-modeled coverage of a typical professional 12″ + horn speaker system in the 1-kHz and 8-kHz bands. (CATT looks at octave bands, not 1/3-octave bands.) Note the narrower coverage at 8 kHz.
Once you’ve made sure the speakers cover the whole seating area with pretty uniform sound, you can check the EQ settings. This is a 2-step process: first, use a test instrument; then use your ears. The instrument can be either an FFT analyzer such as SMAART or Praxis, or an RTA. What’s the difference? Well, there are several. Let’s talk about FFT analyzers first. We’ll look at RTA measurements in a future blog.
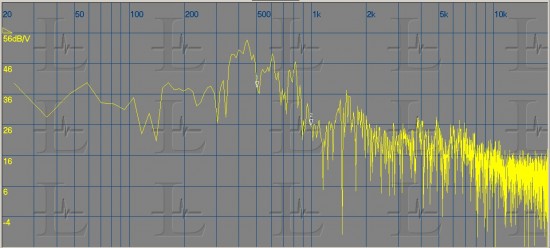
An FFT analyzer can show you frequency response with much finer resolution than an RTA. This may be useful, but not necessarily. To get meaningful results with an FFT analyzer you must time-window your measurement. The window limits the effective resolution of the measurement: if you use a 28.6-millisecond-long window, measurement resolution is limited to a 35-Hz bandwidth. In effect, this limits the usefulness of low-frequency data below at most 35 Hz. (See Figure 2.)
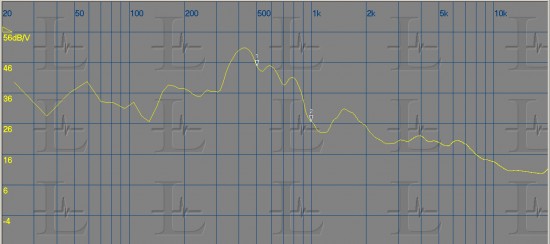
The 28.6-ms window only permits you to see the effect of reflections within about 30 feet of the speaker. You can use a longer window and include more reflections and get better low-frequency resolution. However, the effect of the reflections can create very messy results, as you probably noticed in Figure 2, because of severe peaks and dips from constructive and destructive interference between the direct signal and reflected sound. Yes, there’s more information, but is there too much? The appearance can be cleaned up by smoothing the data. The ear/brain do not seem to be sensitive to small response anomalies less than 1/3 octave wide. (This is a generalization: the ear/brain seems to analyze in critical bands, whose width varies with frequency and SPL, but experience has shown 1/3-octave bands to work well as an approximation.) The response curve of figure 3 shows the results of 1/3-octave smoothing of the Figure 2 curve.
Note that this is not the same curve as would be shown by a 1/3-octave RTA. The primary use of an FFT in evaluating sound-system output is to see the response of a speaker plus early reflections, such as from the ceiling a few feet in front of the speaker. Even though anomalies from reflections will vary from one listener location to another, and thus cannot be equalized out, FFT analyzers can be used to determine whether mitigation is required, such as an absorptive panel applied to the right place on the ceiling. An FFT analyzer is also useful in setting EQ in very reverberant rooms, since the ear is most sensitive to the early sound, and windowing can be used to look at only the early sound. Thus the resulting EQ adjustment can be more nearly optimized for human preferences. Using only RTA measurements to guide EQ settings in a highly reverberant room tends to result in an unnatural-sounding system, since it leads you to use EQ to compensate for the variation of RT with frequency. rh
 Richard A. Honeycutt developed an interest in acoustics and electronics while in elementary school. He assisted with film projection, PA system operation, and audio recording throughout middle and high school. He has been an active holder of the First Class Commercial FCC Radiotelephone license since 1969, and graduated with a BS in Physics from Wake Forest University in 1970, after serving as Student Engineer and Student Station Manager at 50-kW WFDD-FM. His career includes writing engineering and maintenance documents for the Bell Telephone System, operating a loudspeaker manufacture company, teaching Electronics Engineering Technology at the college level, designing and installing audio and video systems, and consulting in acoustics and audio/video design. He earned his Ph.D. in Electroacoustics from the Union Institute in 2004. He is known worldwide as a writer on electronics, acoustics, and philosophy. His two most recent books are Acoustics in Performance and The State of Hollow-State Audio, both published by Elektor.
Richard A. Honeycutt developed an interest in acoustics and electronics while in elementary school. He assisted with film projection, PA system operation, and audio recording throughout middle and high school. He has been an active holder of the First Class Commercial FCC Radiotelephone license since 1969, and graduated with a BS in Physics from Wake Forest University in 1970, after serving as Student Engineer and Student Station Manager at 50-kW WFDD-FM. His career includes writing engineering and maintenance documents for the Bell Telephone System, operating a loudspeaker manufacture company, teaching Electronics Engineering Technology at the college level, designing and installing audio and video systems, and consulting in acoustics and audio/video design. He earned his Ph.D. in Electroacoustics from the Union Institute in 2004. He is known worldwide as a writer on electronics, acoustics, and philosophy. His two most recent books are Acoustics in Performance and The State of Hollow-State Audio, both published by Elektor.