How To Model Audience Absorption

by Richard Honeycutt

This article shed some insights on a method for modeling audience absorption.

Many contractors, and not a few consultants, may not have given much thought to the best method of modeling audience absorption. Back in the early days of manual Sabine calculations, audience seating was characterized in terms of sabins per person. However, it was discovered that more accurate calculations resulted if the size of the seating area was used, its surface area being multiplied by a laboratory-measured absorption coefficient for the type and occupancy level of the seating. Such coefficients are available both for solid seating areas and for those including aisles, with wooden seats, lightly or medium upholstered seats, pews, etc. There are even some values in the literature that distinguish between the effects of summer and winter clothing. The superiority of this method of accounting for audience absorption can be attributed to the wave nature of sound, which makes a large block behave differently than a group of small objects.

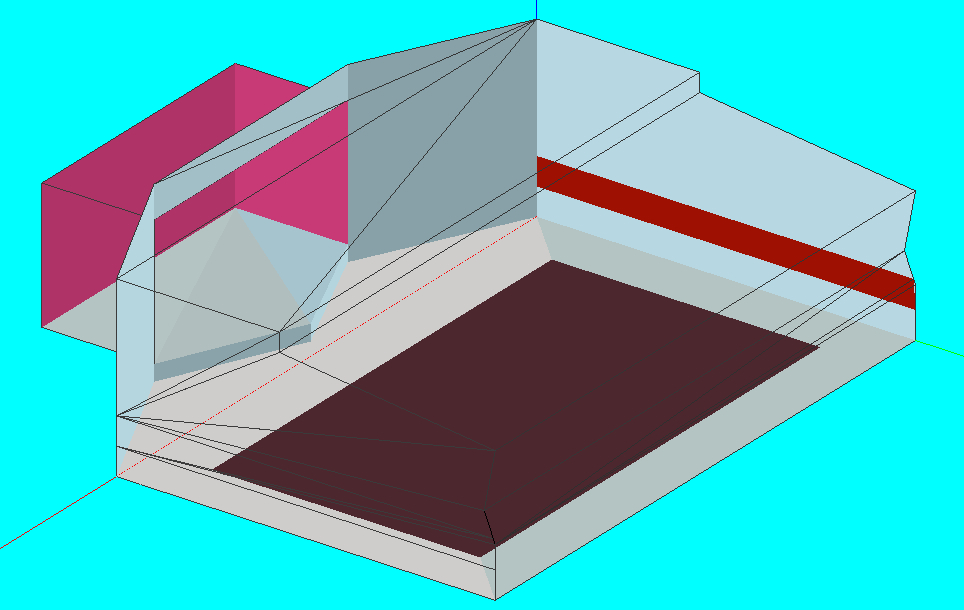
With the advent of computerized acoustical modeling in the last decades of the 20th century, new variables entered the mix. The first application of computerized modeling was for prediction of sound coverage from loudspeakers (as with the Prohs-Harris program), and often just the floor was modeled, with the area to be covered by the audience designated for SPL mapping. Many users simply extrapolated this approach to acoustical models for calculating RT and other acoustical parameters. Indeed, the EASE tutorial from which I learned does not address audience absorption modeling at all, although it does give examples of assigning mapping planes (which EASE calls “audience areas”) to parts of the floor. Figure 1 shows a model with audience absorption modeled in this fashion.

This method, which I have dubbed the “quick-and-dirty” method, clearly understates the audience absorption by ignoring the sides of the audience area, and overstates the volume of the venue by failing to account for the space taken up by the audience. Some users have fallen to the temptation to use the immense calculating power of modern modeling software to “improve” the analysis by inserting individual seats, or individual pews into their models. Such models succumb to the “too much detail” pitfall, which creates inaccurate analyses because of increasing the divergence between the ray-tracing analysis and the wave behavior of the sound. A better method of modeling is to create a block for each group of audience seats, leaving the aisles open. Open aisles have the advantage of allowing the analysis of open reflection paths that may cause problems in the completed venue. In such a model, the audience area extends to the floor, and the floor is cut out beneath the seating area, as shown in Figure 2.

An often-overlooked advantage of computerized modeling programs is the ability to compare ray-traced RT predictions with Sabine analysis. This provides two benefits; the Sabine RT gives a sanity check on the ray-traced results, and it allows a quick calculation of how many more or fewer sabins may be needed to bring the room to its target RT. The first advantage helps us avoid accepting erroneous results caused by faulty modeling (too few rays/particles used) or by persistent flutter echo in the venue. The second one is exemplified by a 200,000 cubic-foot venue whose target RT is 1.5 seconds, and which we have made a first attempt at treating by adding some fiberglass wall panels. The calculated RT is 2.2 seconds empty, using the Sabine method, and 1.6 seconds with treatment. Using ray-tracing, we predict an RT of 2.3 seconds empty and 1.8 seconds with treatment. Examining the echograms, we conclude that we used enough rays for the ray-tracing. The discrepancy between Sabine and ray-tracing must therefore be due to the venue being “non-Sabine-like”: absorption not distributed evenly among floor, sides, and ceiling; and/or the sound in the room not being sufficiently diffuse. Such deviations from the Sabine assumptions are not uncommon. But by using the Sabine equation in reverse, we can find out how much absorption the Sabine calculation saw, and how much the ray-tracing saw:

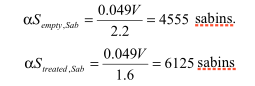
So the Sabine analysis saw 1570 sabins of wall treatment, giving us an RT reduction of 0.6 seconds. This amounts to 2617 sabins per second of RT reduction.
For ray-tracing:

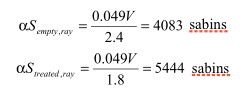
Thus the ray-tracing saw 1361 sabins of wall treatment, mounting to 2268 sabins per second of RT reduction. In other words, each sabin of treatment we add will give us 2268/2671=0.85 sabins of actual RT reduction in a ray-tracing analysis. So since we want to get to 1.5 seconds, a decrease of 0.3 seconds from the ray-trace prediction, we can figure out how much absorption we need to add:

With our initial attempt, ray-tracing saw 5444 sabins, so we now need to increase the absorption by (6533-5444)/0.85=1282 sabins.

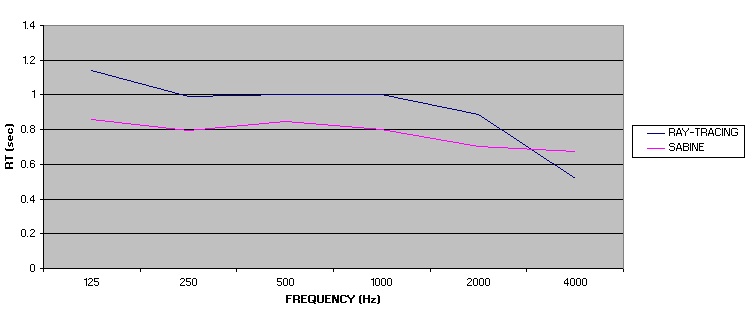
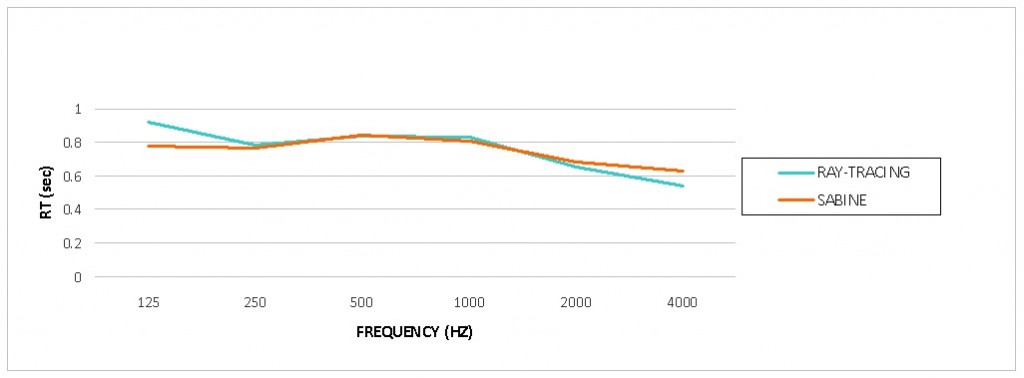
Figure 3 shows a comparison between the Sabine and ray-traced RT predictions for the room whose model is pictured in Figure 1 (quick-and-dirty method). Figure 4 shows the predictions using the better method used in the model shown in Figure 2.

 

You can see that the “better” modeling method gives results more in accord with the Sabine predictions, as we would predict by considering the physics of the situation. In fact, the measured RT of the completed facility agreed well with the results predicted using the “better” method of audience modeling.

The same differences between quick-and-dirty and “better” modeling remained as occupancy was varied, and also showed up in analysis using the same model imported into different modeling software.

Richard A. Honeycutt developed an interest in acoustics and electronics while in elementary school. He assisted with film projection, PA system operation, and audio recording throughout middle and high school. He has been an active holder of the First Class Commercial FCC Radiotelephone license since 1969, and graduated with a BS in Physics from Wake Forest University in 1970, after serving as Student Engineer and Student Station Manager at 50-kW WFDD-FM.  His career includes writing engineering and maintenance documents for the Bell Telephone System, operating a loudspeaker manufacture company, teaching Electronics Engineering Technology at the college level, designing and installing audio and video systems, and consulting in acoustics and audio/video design. He earned his Ph.D. in Electroacoustics from the Union Institute in 2004. He is known worldwide as a writer on electronics, acoustics, and philosophy. His two most recent books are Acoustics in Performance  and The State of Hollow-State Audio, both published by Elektor.