Dynamic Range – More Bits, More Footroom
In this article, Steve Barbar addresses the term bits (numbers) to help the reader get a better understanding of dynamic range.
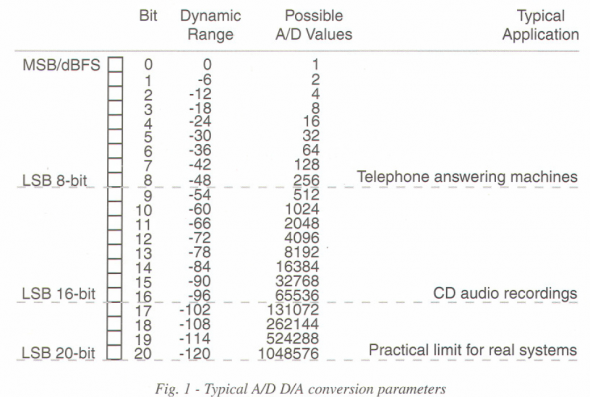
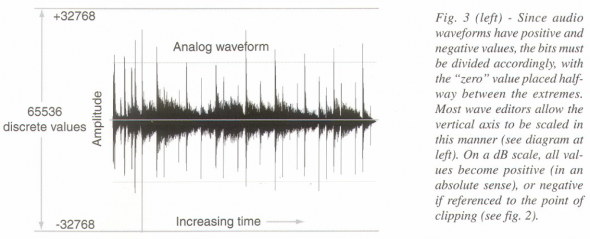
Once converted to a PCM digital signal, there are two fixed points of reference – the Most Significant Bit (MSB), and the Least Significant Bit (LSB). The dynamic range of the digital signal is determined by the number of bits (numbers) that are used to describe the analog signal. The more numbers (bits) the greater the detail in describing the amplitude of the analog source.
Now here’s the part that most people miss – the MSB represents the point at which the digital signal clips HARD – there is no forgiveness.
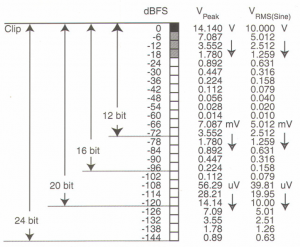
In the digital domain, a signal representing digital full amplitude before clip-operating to the MSB is referred to as dBFS (dB full scale). All other signals can simply be referenced against this value, and will be negative. So adding bits provides more footroom. In other words, we are better able to resolve signals that may mean little to us, depending on what we plan to do with the output. The actual dynamic range is less because LSB contains noise.
In order to provide adequate headroom, one must ensure that the absolute peak value of the analog signal never exceeds dBFS. This means that one must know something about the loudest thing that will ever happen, or if you want to be safe, one must use analog limiting ahead of the Analog-to-Digital (A/D) Converter. Using today’s technology, this reduces the signal-to-noise ratio (SNR) of the digital signal to equal the SNR of the compressor of choice.
Theoretical Example of a 16 Bit System:
Symphony Orchestra – measured peak output 120 – 126 dB at the conductor
A/D clips at +20 dBu =0 dBFS =16 bits
Providing 18 dB of headroom means that the average signal feeding the A/D must not exceed + 2 dBu.
This leaves 12 bits of footroom, or dynamic range, (less than 75 dB) to capture the average signal.
Theoretical Example of a 20 Bit System:
Symphony Orchestra – measured peak output 120 – 126 dB at the conductor
A/D clips at +20 dBu =0 dBFS =20 bits
Providing 18 dB of headroom means that the average signal feeding the AID must not exceed + 2 dBu.
This leaves 16 bits of footroom, or dynamic range, (less than 96 dB) to capture the average signal.
In the real world, the SNR of a VERY good converter (read VERY expensive) does not exceed 110 dB, and rarely makes 106 dB. So the usable-footroom is reduced to less than 80dB.
The next problem is digital gain. In the digital domain, gain is simply a multiplier of a given numeric value. Positive going values decrease headroom against the MSB, and necessarily increase (multiply) the noise floor, as well as the level of any residual DC signals. Adding gain with filters simply does this selectively, and reduces headroom to the MSB selectively. If you increase numeric count beyond the bitwidth of a signal processor, or digital bus, you do not clip the signal as you do in the analog domain. Instead, this will typically “overflow” the processor, and information will be lost. There are no warning lights, bells, whistles -maybe at best an overload indicator at the DfA converter, if you are really juicing something. Unless the hardware is specifically designed to report such a problem, it is unlikely that you will know it, and because multiple gain stages can mask the origin, it can be difficult to track in complex systems.
Generally speaking, when working in the digital domain, making sure that the system of choice has good converters (This means that the ANALOG portion of the converter is as good as it can be – a very good 18 bit converter is FAR better than a poorly designed 20 or 24 bit capable converter) stable firmware and software, and carefully setting gain throughout the system is paramount to optimum operation.
If an AES/EBU digital signal is passed to another digital device of equal or greater bitwidth, the MSB remains the MSB, and the signal will remain unaltered. In the event that the receiving device affords higher bitwidth, again, this will be in the form of additional footroom. sb
Steve Barbar is President of LARES Associates, and a pioneer in electronic acoustic enhancement of,live peiformance venues. Prior, he spent ten years as Advanced Products manager for Lexicon and five years at Systems Wireless Ltd., ,specialists in integrating large numbers of RF devices for televised events.