Using Limiters to Help Protect Loudspeakers
In this article, Charlie Hughes will help you understand how limiters can be used to provide protection from over excursion.
Using limiters to protect loudspeakers is nothing new. In many applications a limiter is placed immediately in front of a power amplifier to keep it from clipping. While this is certainly a good use, there is more that can be accomplished with a limiter to squeeze a bit more low frequency performance out of a loudspeaker while keeping it within is safe operating area.
Most loudspeaker systems have a limited excursion capability. The voice coil and cone assembly can travel only so far before the motor strength significantly decreases, the suspension (surround and/or spider) reaches its limits or both. This excursion limit is generally known as Xmax. With knowledge of the Xmax of a given driver and the displacement response of this driver in a given enclosure it is possible use a limiter to provide protection from over excursion.
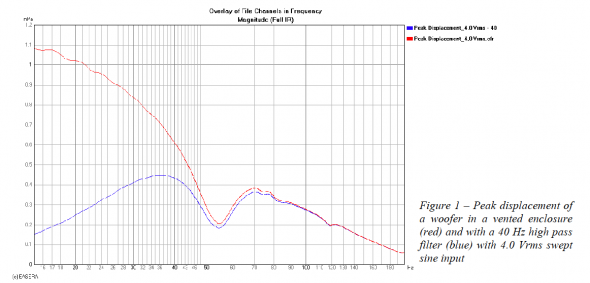
Most low frequency loudspeaker designs have increasing displacement with decreasing frequency. This keeps the SPL output reasonably flat down to the cut off frequency of the system. Below the cut off frequency the SPL decreases while the displacement continues to increase. In Figure 1 we see the displacement response for a 15 inch loudspeaker driver in a vented enclosure. This was measured using an accelerometer, a LinearX LP201 preamp/signal conditioner and EASERA. The y-axis is labeled in mPa (millipascals) but the units are really mm (millimeters). EASERA normally displays the RMS value of signals so the measurement data have been multiplied by 1.414 so that the display will correspond to the peak displacement of the cone as a function of frequency. This measurement was made with an input of 4.0 Vrms (5.66 Vpeak). The dip in the curve at 54 Hz is due to the vented enclosure. In the frequency region of vent tuning the displacement of the driver decreases and will reach a minimum at vent resonance.
For a linear system the displacement response will be directly proportional to the input voltage. This means that the displacement curve can be scaled up or down on the y-axis as the input voltage is increase or decreased. For example, we can see that at 100 Hz the displacement is 0.28 mm with an input of 5.66 Vpeak. If the input is 11.31 Vpeak the displacement at 100 Hz will be 0.56 mm. Doubling the voltage doubles the displacement. At relatively high input voltage the system may no longer remain linear due to power compression (voice coil heating) as well as excursion limitations (both motor and suspension limits). The former is a thermal issue related solely to the RMS voltage of the input signal. The latter is related to the peak voltage of the input signal.
Hopefully the program input signal to the loudspeaker system during normal use has a sufficiently high crest factor that Vrms and Vpeak are separated by at least a factor of four (12 dB). The measurements detailed here use a swept sine with a crest factor of 1.414 (3 dB). Measurement preconditioning to warm-up the loudspeaker voice coil can help to account for thermal compression at higher input voltages. A reasonably high voltage test signal can help to minimize the effects of displacement compression when the displacement response is scaled up.
The loudspeaker driver shown in Figure 1 has a manufacturer’s rated Xmax of 5.0 mm. Usually the displacement can be allowed about 15 – 20 % beyond the rated value before audible distortion becomes problematic. For the purposes of this article we will stick to the manufacturer’s rated value. If we scale this 4.0 Vrms (5.66 Vpeak) measurement by a factor of 5 we can see that the 5.0 mm displacement limit will be reached at approximately 21 Hz with an input of 28.3 Vpeak. Assuming a program signal with a crest factor of 12 dB, this equates to 7.1 Vrms. To put this in perspective, this signal would just be clipping the voltage rails of a 50 W amplifier (into 8 ohms). However, the amp would only be delivering 6.25 W into an 8 ohm load due to the crest factor of the signal.
The point here is that we need to limit the excursion in the low frequency region so we can drive the loudspeaker with higher voltage yielding greater SPL. It is relatively common practice to use a high pass filter to accomplish this. Applying a second order (12 dB/octave) Butterworth high pass filter at 40 Hz results in the displacement response also shown in Figure 1. The displacement maximum is now 0.45 mm at 36 Hz for an input of 5.66 Vpeak. This will allow for a maximum of 62.9 Vpeak to reach 5.0 mm at 36 Hz. In keeping with our reality check perspective above this would just be clipping a 250 W amp. A program signal with a 12 dB crest factor would yield a 15.7 Vrms input (30.9 W into 8 ohms). This is still relatively low.
In order to decrease the displacement in the frequency region below vent tuning so that it is no greater than the displacement maxima above vent tuning (at approximately 70 Hz) requires a second order high pass filter at 50 Hz. This is high enough in frequency to begin to attenuate useable low frequency output from this system. Another drawback of using this high pass filter is that it will add more phase shift (and group delay) to the output of the loudspeaker. This is a vented design so it already has a fourth order high pass response.
Now let’s get back to limiters. This article is supposed to be about limiters isn’t it? For the loudspeaker displacement problem detailed above it would really be nice to be able to limit the displacement without using a high pass filter, or at least one set a lot lower in frequency. But to do this a limiter can’t just limit at a single set level. It must be able to limit lower frequencies at progressively lower levels. Ideally we would like for the limiter to function so that below some frequency, say 45 Hz or so, the displacement response becomes a flat horizontal line. To do this we must alter the signal that is presented to the limiter’s side chain.
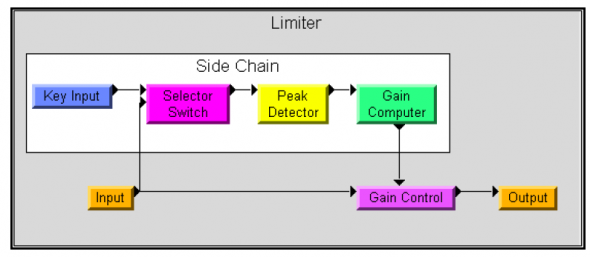
For those readers not familiar, a side chain is the portion of the limiter that computes the gain reduction that needs to occur so that the signal going through the limiter does not exceed the limiters threshold value. This is shown schematically in Figure 2. Typically the side chain receives the same signal present at the input of the limiter. However, it is possible to send the side chain a different signal if the limiter has an external side chain input. This is sometimes called the key input.
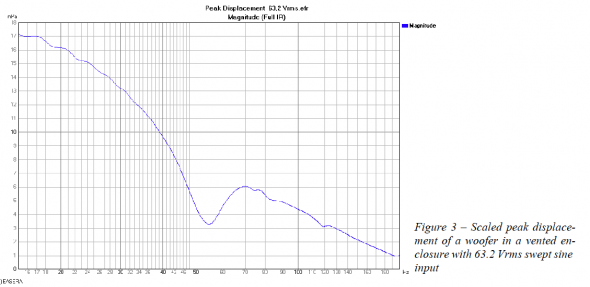
So how do we set all of this up? Let’s say were going to use a 1,000 W amplifier (into 8 ohms) with our loudspeaker system. This amplifier size was chosen so that for a signal with a 12 dB crest factor the maximum output from the amplifier will be 22.4 Vrms (89.4 Vpeak). The input sensitivity required to fully drive this amplifier with a sine wave is 2.0 Vrms (2.83 Vpeak). To keep the amplifier from clipping we need to set the peak threshold of our limiter to +9.0 dBV. This corresponds to the peak voltage of the amplifier input sensitivity. When the amplifier output is at 89.4 Vpeak the loudspeaker displacement response would be close to that shown in Figure 3 if it had no inherent displacement limitation. We can see that the displacement would exceed 5.0 mm below 49 Hz and from 62 – 88 Hz.
This indicates we have to increase the signal level presented to the limiter side chain in these frequency regions. The gain computer of the limiter will then see higher signal levels at these frequencies. This will cause the limiter to reduce the signal level only when these frequencies are high enough to warrant it. The rest of the time the signal is unaltered.
The displacement response is now displayed in dBV (corresponding to the RMS voltage output of the LP201 accelerometer preamp) in Figure 4. We use the RMS value instead of the peak value here because we will be comparing this curve to measurements of some filters. The EASERA measurement system will display measurements based on RMS values unless otherwise scaled. Since our measurement signal is a sine wave this all works out nicely.
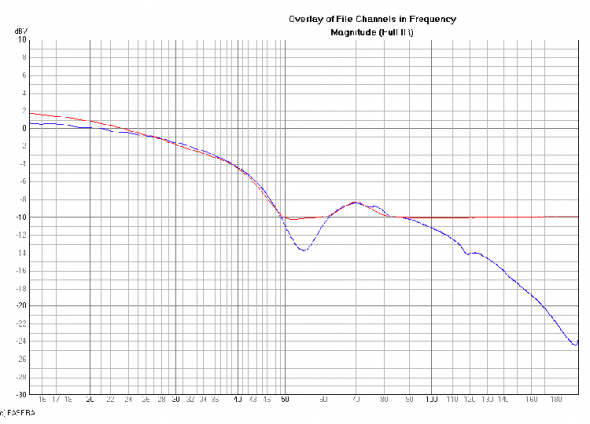
Figure 4 – RMS displacement of a woofer in a vented enclosure (blue) and filter transfer function for limiter side chain (red)
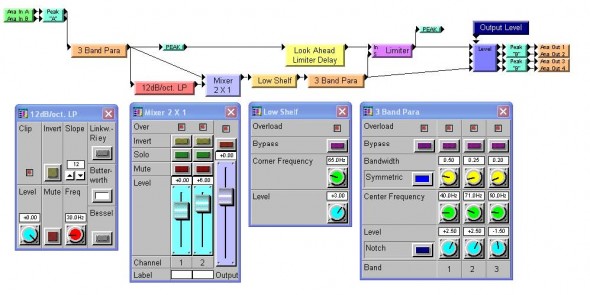
Coincidentally, -10 dBV corresponds almost exactly to the 5.0 mm peak displacement shown in Figure 3. Anything above -10 dBV needs to be limited to -10 dBV in order for the displacement not to exceed 5.0 mm. Several filters are set-up to yield the transfer function also shown in Figure 4. The signal that will be presented to the side chain of the limiter will pass through these filters. The signal flow for this is shown in Figure 5. The filters used are a second order shelving filter (low pass and mixer), a first order shelving filter and a 3 band parametric EQ. These filters will increase the level of the signal in a manner corresponding directly to the desired frequency dependent limiting in order to control the woofer’s displacement.
The only thing remaining is to set the threshold of the limiter and measure the displacement of the woofer with the new limiter processing in place. Since I want to show only the effects of the limiter and not any potential nonlinearity in the suspension or motor of the woofer in decreasing the woofer’s displacement, I will not test at 89.4 Vpeak. I do this also because I like my neighbors, I think they like me (although I may be delusional) and I would like things to stay this way, I think. Instead I will test at 4.0 Vrms (5.66 Vpeak) and scale the displacement as if it was tested at the higher voltage. To accomplish this all I need to do is adjust the threshold of the limiter so that it limits at 5.66 Vpeak. This should be done either with the side chain filtering bypassed or at a frequency much higher than would be affected by these filters.
Because we are now using a limiter, the system under test is no longer linear, time invariant (LTI). For this reason FFT measurement techniques, such as those in EASERA and other similar measurement systems, can no longer be used to accurately measure this system. Instead, a steady state sine wave at a fixed frequency is used. The results are recorded and plotted in an Excel spreadsheet. Measurement points for different frequencies are at 1/12 octave spacing. The results are shown in Figure 6.
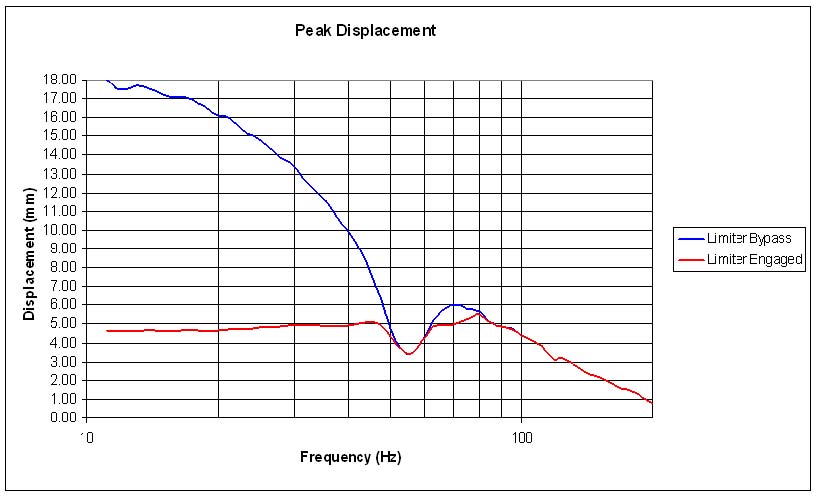
Figure 6 – Scaled peak displacement of a woofer in a vented enclosure with a nominal 63.2 Vrms sine input; limiter bypassed (blue) and limiter engaged (red)
Here we can see that with the limiter bypassed the displacement is almost identical to that shown in Figure 3. This is expected. With the limiter engaged the displacement does not exceed 5.0 mm except for a small region around 80 Hz. This is due to the filters feeding the limiter side chain not being an exact match to the displacement curve in this frequency region. This can also be seen in Figure 4.
One of the additional benefits of this type of low frequency excursion limiting, as opposed to a high pass filter, is that boost EQ can be applied at low frequencies if desired. At lower signal levels this EQ may subjectively improve the sound of some loudspeaker systems. The limiter we have implemented will reduce this EQ boost when the signal level is sufficiently high that it would cause the amp to clip or the driver displacement to exceed its recommended range. In essence, this limiter will remove the EQ momentarily, only at the very highest signal levels containing low frequency energy, and then return the EQ when these high level peaks have decreased below the threshold. When implemented correctly, this can be very transparent and yield good results.
Many thanks must go to Ray Rayburn for his valuable insight and patient discussions with a very green engineer many, many years ago on this topic. ch