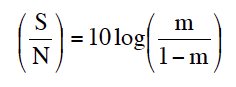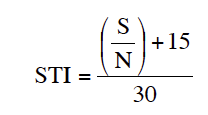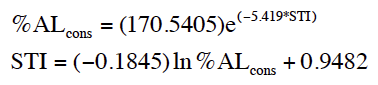A Do-it-Yourself Guide to Computing the Speech Transmission Index
In this article, Farrel Becker shares the steps required to compute the Speech Transmission Index (STI) from a measured impulse response.
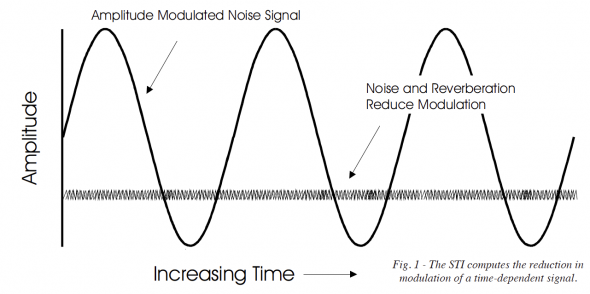
The Speech Transmission Index (STI) is a method of measuring speech intelligibility in noisy and/or reverberant environments. Since human talkers modulate a stream of air from the lungs with the vocal cords, good communication systems must preserve this modulation when delivering speech information to a listener. Farrel Becker, a sound engineer and computer programmer for Crown International spends much of his time programming computers to perform tasks that once had to be executed using labor intensive analog methods. In this Tech Topic he shares with us the steps required to compute the STI from a measured impulse response. With a number of economical methods available today to measure impulse responses, this look at the STI becomes quite relevant. pb
The Speech Transmission Index (STI) and its little brother the Rapid Speech Transmission Index (RASTI) are computed from an impulse response via the modulation transfer function (MTF). The MTF is defined as the magnitude of the Fourier transform of the squared impulse response divided by the total energy in the impulse response. Okay, so here we go step by step starting with a full bandwidth impulse response. As long as we use a valid method, how we obtain the impulse response doesn’t matter. It could be done using MLS, dual channel FFT, balloon pop, hand grenade or hydrogen bomb. Don’t ask, don’t tell.
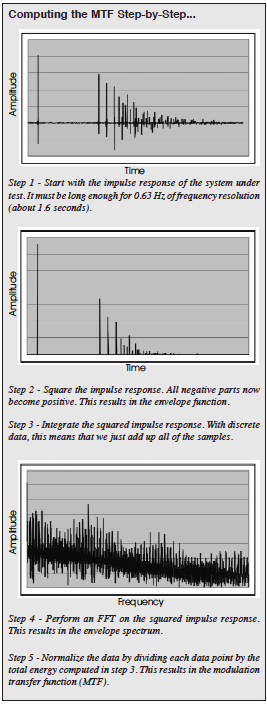
1. Square the impulse response. This gives us the envelope function. Graphically, this has the data in the negative half of the impulse response (the part that goes below zero) flipped up to the positive half. Now the entire impulse response is positive and above the zero line. Also the peaks are all higher because their values have been squared.
2. Integrate the squared impulse response to get the total energy. We’re basically just adding up all of the levels (samples) on an energy basis, not in dB (10^(dB/ 10)).
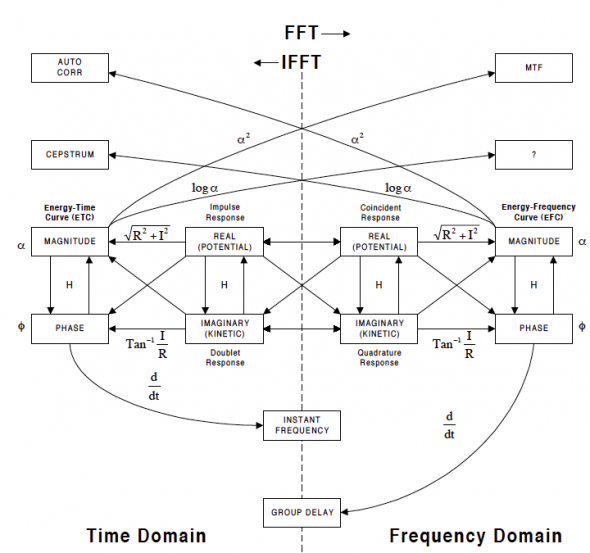
3. Compute the Fourier transform of the squared impulse response. The Fourier transform, as usual, is converting a function in the time domain to a function in the frequency domain. When using a computer we usually, but not always, use the Discrete Fourier Transform (DFT) algorithm. We are most familiar with using the DFT to convert an impulse response to a frequency response. (We can also go in reverse and convert a frequency response to a time response as is done in dual channel FFT analyzers.) However, we are transforming a squared impulse response so we don’t end up with the usual frequency response. Instead we end up with a thing called the envelope spectrum. For those of you who remember the old domain chart that we used to use(see fig. 2), the envelope function is one of those functions that used to have a question mark in its box.
4. Normalize the envelope spectrum, the FFT of the squared impulse response, by dividing it by the total energy in the squared impulse response. We already computed the single number total energy in step 2 so now we divide each of the data points in our FFT output by this number and at last we arrive at the modulation transfer function. The output of the FFT is complex so what we have is the complex MTF. (No, its not complicated. It has both real and imaginary parts. If you can’t imagine what I mean by imaginary parts, just use your imagination.) What we want is the magnitude of the MTF so for all of our data points…
5. Take the square root of the sum of the real part squared and the imaginary part squared. Graphically, we now would have a plot of modulation index (vertically) which runs from 0 to 1 versus modulation frequency (horizontally) which runs from 0 to 1/2 of the sampling frequency that was used to gather the original impulse response data. Okay. Now we know how to get the MTF. So now on to the STI. For an STI we need the MTF for each octave band from 125 Hz to 8 kHz.
6. Take the full bandwidth impulse response, run it through octave band filters (digital of course) and for each octave we compute the MTF using steps 1 through 5. We now have 7 octave band MTFs.
7. Now with each of the octave band MTFs we take the amplitude at 14 modulation frequencies spaced 1/ 3 of an octave apart starting at 0.63 Hz and going up to 12.5 Hz. Yes we start at 63 hundredths of a Hz and go up to 12.5 Hz. These are the so called “m” values, m for modulation. With 14 m values (one for each of the 14 modulation frequencies) from each of the 7 octave band MTFs we get a total of 98 m values. (The “matrix” of m values can be seen in Sound System Engineering page 248.) Remember, even though the MTFs were generated from octave band filtered impulse responses, the MTF frequency scale still runs from 0 to 1/2 of the sampling frequency that was used to gather the original impulse response data. Because we took the FFT of the squared octave band filtered impulse response instead of the raw octave band filtered impulse response, we get something with a shape that is completely different from a conventional frequency response.
8. We now convert each of the 98 m values into an “apparent signal-to-noise ratio” (S/N) in dB. As we are all Syn-Aud-Con grads, we know that noise affects speech intelligibility. Well it also causes a reduction in modulation (by filling in the gaps) and shows up in the MTF. Reverberation has the same effect on the MTF, hence the term apparent signal-to-noise ratio. Well I haven’t written any equations so far but we now come to some that are unique to the task at hand so for those who want all of the details the conversion is performed by the following equation:
The S/N above is in parenthesis to indicate that it is the apparent S/N and not the true S/N in the room.
9. Limit the Range. The (S/N) must be limited to a 30 dB range so any value greater than 15 dB is set equal to 15 dB and any value less than -15 dB is set equal to – 15 dB.
10. Compute the mean (S/N) for each octave band. We have 14 values for each octave band so we just add them up and divide by 14. Now we have 7 mean (S/N) values, one for each octave band.
11. Weight the octave mean (S/N) values and compute the overall mean (S/N) from the 7 weighted octave means. Instead of adding up the 7 values and dividing by 7, this time we perform a weighted average. With ordinary averaging, we add up the values and then divide by the number of values. In step 10 we added up 14 values and then divided by 14. We could have just as easily divided each of the values by 1/14 and then add them up. The result is the same. With weighted averaging, some of the numbers are multiplied by a greater number than others. The values that are multiplied by the greater numbers are given a greater importance or “weight” in the average. In ordinary averaging, all of the values are given equal weight. With weighted averaging we are giving more weight to some values than we are to others. The key here is to be sure that the multipliers, or “weights” are all less than 1 but all added up together equal 1. So here we weight the mean (S/N)s for each of the octave bands as follows: 125 Hz 0.13, 250 Hz 0.14, 500 Hz 0.11, 1 kHz 0.12, 2 kHz, 0.19, 4 kHz 0.17 and 8 kHz 0.14. Notice that the 2 kHz octave band is given the greatest weight. We are interested in speech intelligibility after all. So we weight the mean (S/N)s that we computed in step 10 for each octave band by multiplying them with their respective weights and add up the results to arrive the at overall mean (S/N).
12. And finally, we convert the overall mean (S/N) to an STI value by taking the overall mean, adding 15 to it and dividing the result by 30 thus:
Well it seems like a long road to travel from impulse response to STI and I guess it is. This is why our computers hesitate a bit when asked to compute and display the STI. Well at least they used to before we had 330 MHz Pentium IIs. Okay. So now we know all about the STI. What about RASTI? You recall that RASTI stands for RApid Speech Transmission Index. It is basically a short form of the STI intended as a means to quickly estimate speech intelligibility. The speed comes from analyzing only 2 octave bands (500 Hz and 2 kHz) instead of the 7 in the STI. Also, instead of using 14 modulation frequencies for each band as we did in the STI we only use 4 for the 500 Hz band and 5 for the 2 kHz band. So, to compute the RASTI, we obtain a modulation transfer function using steps 1 through 5 above for both the 500 Hz and 2 kHz octave bands. Next we follow steps 7 through 13 to compute the RASTI but with a couple of differences. First, for the 500 Hz octave band we only use 4 modulation frequencies spaced an octave apart starting at 1.0 Hz and going up to 8.0 Hz. For the 2 KHz octave band we only use 5 modulation frequencies spaced an octave apart starting at 0.7 Hz and going up to 11.2 Hz. Next, instead of using weighted averaging to compute the overall mean (S/N) as we did in step 12, we use ordinary averaging. We just add the 2 octave band (S/N)s together and divide the result by 2. After obtaining the overall mean (S/N), we convert it to RASTI using the same equation as in step 13: RASTI = ((S/N) + 15) / 30. That’s it. The RASTI value is intended to be a short cut because it used to take so long to compute the STI. In fact, one manufacturer actually produced a dedicated pair of boxes (a transmitter and a receiver) to automatically measure RASTI utilizing a special test signal. This is the system that comes in green boxes and sounds like a “choo choo train.”
Now, what about obtaining the STI and RASTI values using TDS? Well with TDS we start out with an Energy Time Curve (ETC). What is an ETC? It is essentially the envelope function we computed in step 1. So we skip step 1 and press on with the analysis. The only real difference is that instead of starting with a single full bandwidth impulse response and then filtering it into 7 individual octave band impulse responses, we actually measure 7 individual octave band ETCs. So we skip over step 6. That’s all there is to it. There are some fine points to consider when using the STI and RASTI. First of all, remember that we need to be able to get the m value at 0.63 Hz. This means that we need an impulse response of sufficient length—about 1.6 seconds. Shorter impulse responses can work reasonably well as long as they are longer than the room’s reverberation time. This, of course, is usually a requirement for MLS. Also, we should member that the STI and RASTI are based on S/N ratios. While reverberation also affects S/N, and in sound system work is almost always the sole cause of any problems, the STI/ RASTI process converts the effects of reverberation to an apparent S/N. This is okay since we can measure reverberation quite well. However, when we use techniques such as TDS and MLS to gather our data, we have strong noise immunity in our measurement systems. This means that the true S/N of the room is not being measured and included on the computations. This why some systems allow for the operator to enter noise values manually or to use measured octave band noise values from, for ex- ample, an NC measurement. And, finally, yes, as John Murray pointed out on the listserv, I did come up with a conversion from STI to %ALCons and back.
A conversion chart based on these equations along with the STI/RASTI subjective scale can be found on page 248 of Sound System Engineering sec- ond edition. Well, I hope that makes it all at least a little bit clearer. Fortunately, we don’t necessarily did to know how some of our tools work on the inside in order to make good use of them. After all, everyone can use a pay phone but how many know what’s going on inside? fb