Small Room LF Design Dimensions or Ratios?
For at least the past 6 decades, acousticians have sought better sounding small rooms. Over the last 10 to 15 years, the “home studio” and “home theater” technology boom has brought the question of “What size/shape should my room be?” back to the forefront. There are many, many great papers written on this topic. A list is included at the end of this Tech Topic. There is little argument that these papers have helped designers create better acoustical spaces. What is arguable is whether the “ideal” ratios are, in fact, “ideal.” Some of the “ideal” ratios were developed using dated methods and computational tools. Sometimes, good room ratios were just a designer’s dumb luck. With today’s computational abilities and knowledge of what is actually feasible for a small room design, we should be able to develop a tool that can quickly evaluate a range of good dimensions for any small room.
What’s wrong with the “ideal” ratios? A few things:
- – The volume dependence of many of these ratios also places undue constraints on the designer of a “real” room.
- – Another hurdle is the fact that these “ideal” ratios are often difficult to implement in practical room design situations. They may also be undesirable for non-acoustical reasons.
- – Yet another hurdle is, even though the list of ratios used is short, which will be “the best” for a given room?
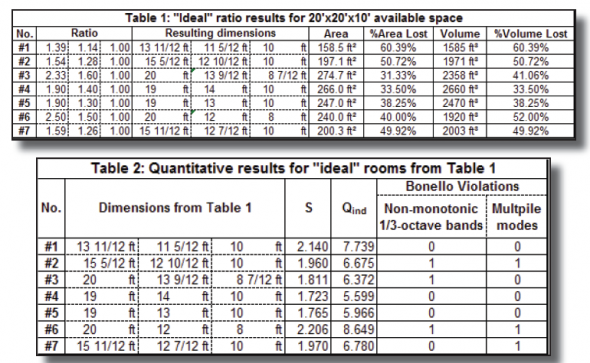
Let’s look at an example: A designer is approached to provide a good sounding studio room in an existing space that is 20’x20’x10’. Assuming we can use the full length, width, or height, we can apply the list of “ideal” room ratios as shown in Table 1. (Note: This list is of “ideal” ratios is taken from Everest’s Master Handbook of Acoustics, 3rd edition, Table 13-2.) But how do we choose “the best” from Table 1? Certainly, a client looking for his money’s worth in terms of leased square footage would opt for #3 or #4. But is that acceptable? Is that the best the designer can do?
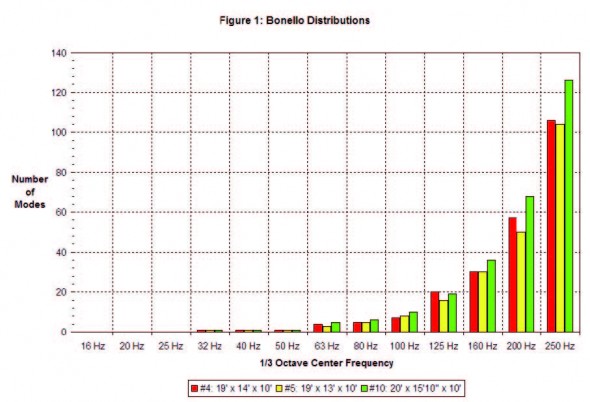
Table 2 provides the dimensions from the above analysis with their corresponding quantitative results. The Louden S, Walker Qind and Bonello violations will all be explained shortly. Suffice to say, #4 and #5 look to be the best. Figure 1 shows the Bonello distributions for these two choices.
Having presented a list like this to the owner, they may very well be impressed. They may not be pleased, however, that 31.3% of the square footage for which they are paying is being wasted. If rent is, say, $10/ft²/month, they’ll be “wasting” about $150,000/year. The responsible thing would be to ensure the owner is getting the most for their money. So, the question that remains: Are there any other dimensions that will work? Particularly dimensions that will maximize the use of the available area?
More useful tools
RPG’s Room Sizer™ computer program is an extremely useful tool in this regard. By analyzing a room’s geometry as well as the layout of listener and loudspeakers in the room, this program enables a user to develop the best possible room and setup for their listening needs based on the modal and speaker-boundary interference responses.
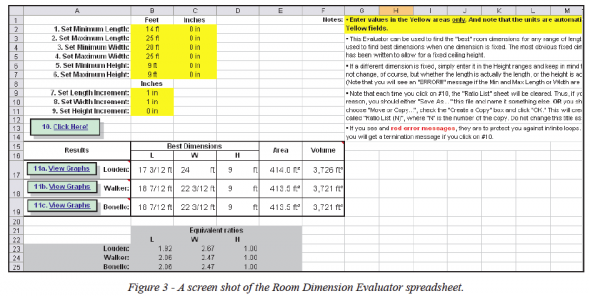
In the pursuit for additional useful tools, a basic spreadsheet has been developed (Figure 3) that uses some of the common design criteria that were put forth in the various papers listed at the end of this Tech Topic for dimensional evaluation. Whether or not a dimension such as length, width, height, or volume is fixed, the criteria can be used to determine good dimensions to use. (By fixing one of these variables, the aforementioned “ideal” ratios were developed. Unfortunately, there has been, in this author’s opinion, too much emphasis on the results—the ratios. Not enough emphasis has been placed on the methods—calculating modal density parameters for different sets of good room dimensions). The criteria established in the spreadsheet are:
- 1. Louden’s standard deviation, “S” be as low as possible.
- 2. Walker’s Room Quality Index, “Qind” be as low as possible.
- 3. And Bonello’s two criteria of:
- a. Monotonically increasing modal density in 1/3-octave bands and
- b. No overlapping modes in 1/3-octave bands containing 5 modes or less.
Louden’s S is a good statistical criteria that looks at modal density. Walker’s Qind is very similar to Louden’s S: It is a simple mean-square modal density calculation. The Bonello criteria are very easy to evaluate and have proven useful in the design of many small rooms.
This spreadsheet allows the user to evaluate ranges of dimensions in whatever increments are desired. While the calculation time can be rather long, the hope is that careful selection of the ranges will ensure the process only has to be run once. The resulting table of dimensions, S, Qind and Bonello violations is designed to be quite useful. All criteria, along with comparisons to room volume and floor area, can be looked at exclusively or in combination. The “List” provides for a complete analysis of all the possibilities within the parameters that have been set.
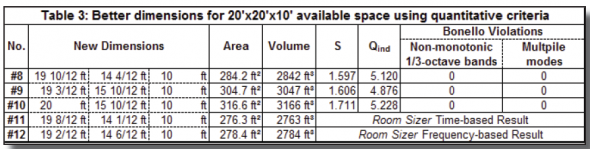
So getting back to our example, the desire is to maximize the space and be sure the low frequency response will be the best it can be. At the same time, the owner wishes to get the most bang for their buck in terms of rent. Taking the 1.9:1.3:1.0 ratio as our minimum and assuming we wish to use all 10’ of the ceiling height, the spreadsheet yielded the results shown in Table 3.
From the above, it should be apparent that the “ideal” ratios did not provide us with “the best” results. All of the results in Table 3 are quantitatively better than #3, #4 and #5 from Table 2. And in the case of #10 above, the wasted area only amounts to 20.8%. Congratulations! You just saved the owner over $50,000/year!!!
Note that I have included a time-based and a frequency-based set of room dimensions calculated from Room Sizer in #11 and #12 for comparison purposes. I have also included the Bonello distribution of #10 in Figure 1.
If the evaluation were run again, this time with a varying height, more useful dimensions could be added to this new list. 
Finally, a simple add-on spreadsheet to the main Room Dimension Evaluator can generate contour plots similar in nature to those generated by Milner and Bernhard (1989), as well as by Cox, D’Antonio and Avis (2004). Figure 2 shows an example of a contour plot generated for the example 20’x20’x10’ available space we looked at earlier. The contour plot gives a quick visual reference to the normalized Louden standard deviations calculated by the main spreadsheet. The normalization simply compares all S values to the maximum and minimum values and rates them from 0.00 to 1.00, with 0.95-1.00 being consider “ideal.” (Appearing as the black areas in Figure 2.) With a set 10’ height, “ideal” dimensions can be quickly read off the plot without having to repeat the calculation process.
Conclusions
A paradigm shift regarding small room dimensional evaluation is in order. As designers, consultants and contractors asked to provide the best possible results for a customer, a simple tool that provides as much flexibility as possible for small room design should be implemented. The results obtained using the spreadsheet discussed (available for download from www…) can help the designer maximize both the acoustical and the practical needs for a space. By evaluating all the possibilities in terms of useful room dimensions—and avoiding the pitfalls of possibly mis-applying “quickie” room ratios—the best possible economical, ergonomic (everyone likes to work in a bigger room), and acoustical space can be designed.
Acknowledgments
A big thank you to Eric Desart, Jeremiah Flaherty, John Griggs, Gavin Haverstick, Jeff Madison and Neal Thompson Shade for their valuable assistance. The Room Dimension Evaluator Spreadsheet is available for download at
http://www.auralex.com/savant/RDE/
Bibliography
Frequency Distribution of Eigentones in a Three-Dimensional Continuum by Richard H. Bolt, Journal of the Acoustical Society of America (JASA), Volume 10, January 1939, pp 228-234.
Distribution of Eigentones in a Rectangular Chamber at Low Frequency Range by Dah-You Maa, JASA Volume 10, January 1939, pp 235-238.
Normal Modes of Vibration in Room Acoustics: Angular Distribution Theory by Richard H. Bolt, JASA Volume 11, July 1939, pp 74-79.
Analysis of Sound Decay in Rectangular Rooms by F.V. Hunt, L.L. Beranek and D.Y. Maa, JASA Volume 11, July 1939, pp 80-94.
Normal Modes of Vibration in Room Acoustics: Experimental Investigations in Nonrectangular Enclosures by Richard H. Bolt, JASA Volume 11, October 1939, pp 184-197.
Frequency Distribution of Normal Modes by Glenn M. Roe, JASA Volume 13(1), July 1941, pp 1-7.
Polycylindrical Diffusers in Room Acoustic Design by John E. Volkmann, JASA Volume 13, January 1942, pp 234-243.
Performance of Broadcast Studios Designed with Convex Surfaces of Plywood by C.P. Boner, JASA Volume 13, January 1942, pp 244-247.
Normal Frequency Spacing Statistics by Richard H. Bolt, JASA Volume 19(1), January 1947, pp 79-90.
Note on Normal Frequency Statistics for Rectangular Rooms by R.H. Bolt, JASA Volume 18(1), July 1946, pp 130-133.
Acoustical Field at Normal Modes in Rooms by T.S. Korn and R. Van de Plas, JASA Volume 29(12), December 1957, pp 1267-1270.
Computed Frequency and Angular Distribution of the Normal Modes of Vibration in Rectangular Rooms by L.W. Sepmeyer, JASA Volume 37(3), March 1965, pp 413-423.
Dimension-Ratios of Rectangular Rooms with Good Distribution of Eigentones by M.M. Louden, Acustica Volume 24, 1971, pp 101-104.
A New Criterion for the Distribution of Normal Room Modes by Oscar Juan Bonello, Audio Engineering Society (AES) Preprint No. 1530, November 1979.
An investigation of the modal characteristics of nonrectangular reverberation rooms by Joseph R. Milner and Robert J. Bernhard, JASA Volume 85(2), February 1989, pp 772-779.
Optimum Dimension Ratios for Small Rooms by R. Walker, AES Preprint No. 4191, May 1996.
Room Sizing and Optimization at Low Frequencies by Trevor J. Cox, Peter D’Antonio and Mark R. Avis, JAES Volume 52(6), June 2004.
The Master Handbook of Acoustics, 3rd edition by F. Alton Everest, McGraw-Hill, 1994.
Microsoft Excel 2002 Visual Basic for Applications Step by Step by Reed Jacobson, Microsoft Press, 2001.