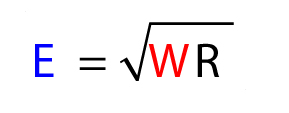Power Ratings Use and Abuse
by Pat Brown
Is a power rating for the sales force or for the system designer?
“One number” power ratings for both loudspeakers and amplifiers are now accepted at face value and seldom questioned. Large numbers are tossed around, often without details as to “why” the product has a particular rating. This has caused an escalation in rated values that in some cases are laughable. It is a good exercise to walk through an example case to better understand how to interpret a loudspeaker power rating.
The Method
It was determined by measurement that the maximum input voltage Emax to a loudspeaker is 20 Vrms (IEC noise) for 3-minutes duration. This is a “limit” rating, and can be taken “as is” or expressed as a power rating. There are two equations for determining the power rating (Fig. 1). The first requires knowledge of the voltage and the impedance (simplified to an equivalent resistance). The second requires knowledge of the voltage and the current.

Equations 1 and 2 – Power calculations from voltage, current, and resistance
Figure 1 (top plot) shows the impedance magnitude (Z) curve for the loudspeaker. The bottom plot shows the 1/3-oct average as displayed in the Common Loudspeaker Format viewer. What is the value of the impedance? There are three possibilities.
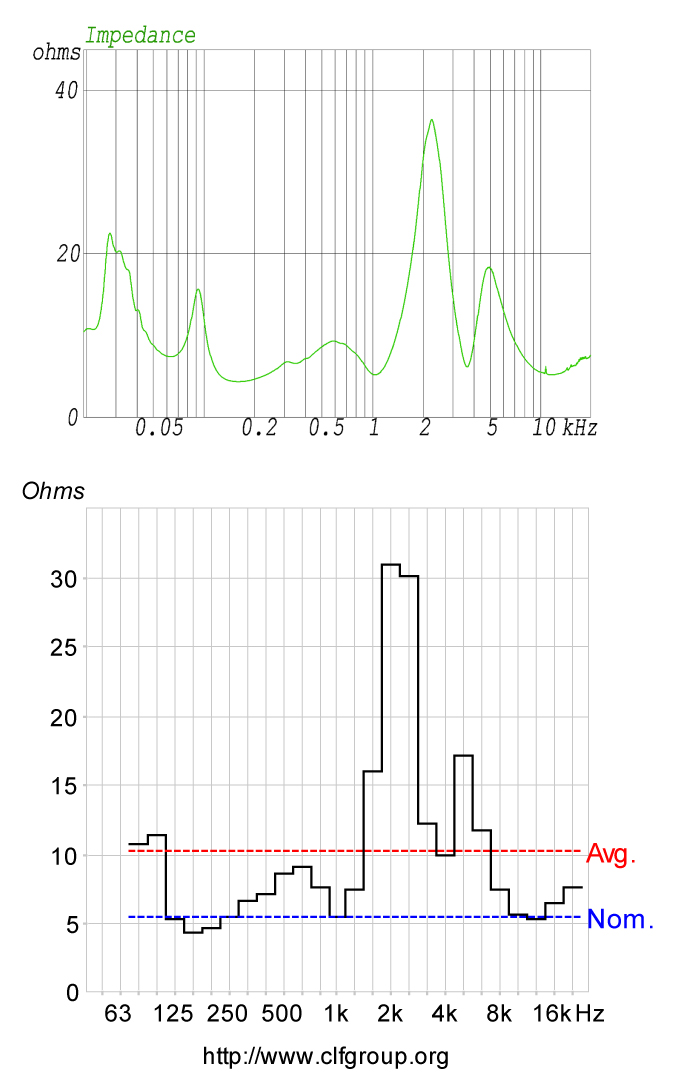 Figure 1 – The impedance plots of the loudspeaker
Figure 1 – The impedance plots of the loudspeaker
The minimum impedance (Zmin) is 4.4 ohms, occurring at 157 Hz.
The rated impedance (Zrated) is 5.5 ohms. This is Zmin times 1.25.
The average impedance (Zavg) is 10.2 ohms.
Which impedance should be used to calculate the rated power?
Using Zmin the power rating is 91 watts.
Using Zrated the power rating is 72 watts.
Using Zavg the power rating is 40 watts.
Power Based on Current Draw
Next, I used a current shunt to measure the actual current flow at Emax. Figure 2 shows both the measured amplifier output voltage (20 Vrms) and the voltage across the current shunt (194 mV) at Emax. The shunt resistance is 0.1 ohms. From ohm’s law (I = E/R) the current is 1.9 amperes. The power rating, using the second power equation, is 40 watts.
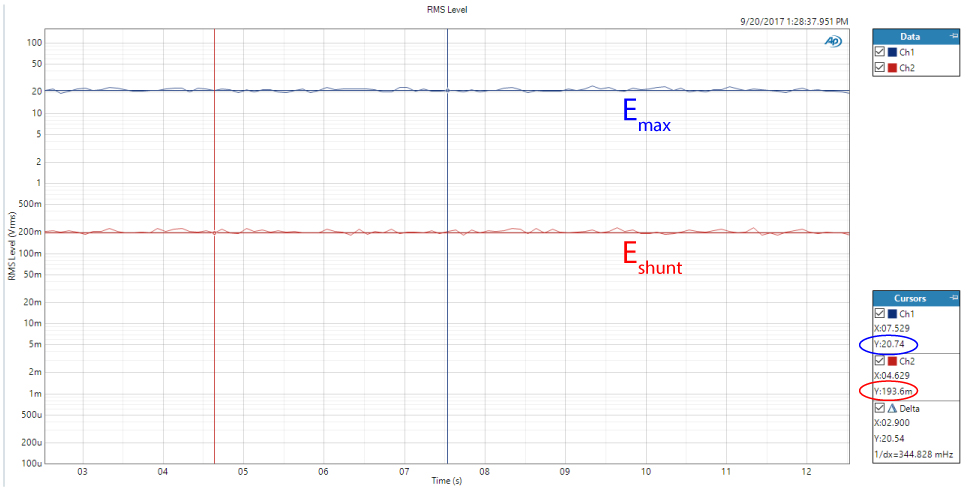 Figure 2 – Time domain plot showing Emax and Eshunt (10 seconds of 180 seconds)
Figure 2 – Time domain plot showing Emax and Eshunt (10 seconds of 180 seconds)
So, for broad band program material, the amplifier sees the average impedance of the load. For a narrow band signal, such as a sine wave, the amplifier can see any value on the impedance curve. The purpose of Zrated is two-fold:
- To simplify the impedance curve to a “one number” rating
- To prevent the manufacturer from over-stating the loudspeaker’s impedance. If a 4 ohm loudspeaker is given a Zrated of 8 ohms, the user may be inclined to drive two in parallel from a single amplifier channel.
Voltage – The Common Denominator
Note that the common denominator between the power calculation methods is Emax. It is measured precisely and cannot be disputed. Expressing it as a power rating ushers in ambiguity. A loudspeaker power rating is only useful if Emax can be calculated from it (Equation 2). There is marketing pressure to publish the highest possible power rating. There is a penalty in the marketplace for publishing a conservative power rating. This can lead to some major problems for end users. Let’s consider some scenarios.
Equation 2 – Calculating Emax from a power rating
Scenario 1
The manufacturer uses Zmin to calculate the power rating (91 watts) and rounds Zrated to the nearest common value (8 ohms). If the end user calculates Emax from these two values they will get 27 Vrms. This will exceed the loudspeaker’s thermal limit and likely result in damage.
Scenario 2
Zrated is used to calculate the power rating (72 watts). The power amplifier GUI allows the power output of the amplifier to be monitored in real time. The end user drives the loudspeaker to 72 watts. This puts 27 Vrms across the loudspeaker, again exceeding Emax.
Scenario 3
The Emax of the loudspeaker is 20 Vrms. If it is necessary to drive the loudspeaker to this RMS voltage, a much larger amplifier will be required. 12 dB is a reasonable peak room margin, which means that the amplifier will need to be able to pass 80 Vrms for signal peaks. The sine or burst test rating for such an amplifier would be nearly 400 W into 8 ohms. An amplifier with this rating would be capable of destroying the loudspeaker, since its output voltage could easily exceed 20 Vrms with highly compressed program material. In an attempt to get the customer to buy an appropriately sized amplifier, the manufacturer gives the loudspeaker a power rating of 200 W, and suggests that they buy an amplifier twice that size – which produces a perfectly justifiable end result. Thinking the loudspeaker is rated at 200 W continuous, the user blows up the loudspeaker.
Scenario 4
In addition to the power rating, the manufacturer publishes Emax. When the system is commissioned, the technician configures an RMS limiter in the amplifier to engage just below this value. The maximum possible SPL is achieved, and the loudspeaker is in no thermal danger.
Conclusion
The loudspeaker in this study can handle 20 Vrms of IEC noise for 3-minutes. Regardless of the power rating, the Emax is 20 Vrms. Converting the Emax to watts requires the use of an impedance value. Since the impedance is somewhat arbitrary, so is the resultant power rating. Incorrect assumptions on the part of the end user can easily result in overpowering the loudspeaker.
Loudspeaker power ratings at face value have little practical use beyond selling the loudspeaker. It is very dangerous language to say that a loudspeaker can “handle” X watts or an amplifier can “put out” X watts. A meaningful loudspeaker power rating will allow the determination of Emax, which can be easily monitored and regulated to protect the loudspeaker. This will also allow the selection of an appropriate amplifier to drive the loudspeaker, given the peak room requirements for the application.
The power rating for an amplifier or loudspeaker is a concise way of representing the performance characteristics of a product. Both involve voltage, current, impedance, and time. The power equations allow these parameters to be expressed concisely as a single wattage value. This is fine, so long as sufficient information is given to run the math in reverse to harvest the original voltage, current, and impedance values from the rating. This is seldom the case, and the result is a ratings arms race to sway the buying public. We will continue to lobby for good engineering practices for establishing meaningful power ratings for audio products. pb