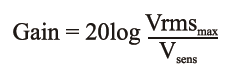Meaningful Metrics – The Use and Abuse of Loudspeaker Power Ratings

By Pat Brown

Pat Brown brings some clarification to loudspeaker Power Ratings.

Introduction

A few years have passed since I last produced an article on this subject. In that time I have continued to power test loudspeakers of all types on a regular basis and have refined some techniques for doing so. These methods have been used in my loudspeaker profiles for Live Sound International magazine, exposing them to the scrutiny of the audio community. I have had numerous reports from manufacturers and individuals who have found value in the methods and who have implemented the techniques and concepts in their own testing. The most satisfying reports are from those who have used them for field testing, which was the original motivation for the techniques.

The test of time tends to either reinforce a methodology or reveal its shortcomings. While I have not found the need for any fundamental changes to the procedures, I can add some clarity regarding the motivation for testing and the use of the results. I will not include the details of the power test method here, as they are available for free download from http://www.etcinc.us/articles-sac.htm.

Standards

While standards exist for loudspeaker power testing, exact procedures are usually not given. This allows the investigator some latitude in implementation. My objective is not to create a new Standard or contradict the existing ones. Instead it is to bring clarity to the subject by outlining some exact methods for conducting the tests using readily available instrumentation as well as to provide insights into how to use the results. It is my intent that this body of work will aid in clarifying existing Standards as well as help the end user to interpret and apply the resultant specifications in the system design and calibration processes. Some of the Standards have existed for decades, yet confusion still remains regarding the sizing of amplifiers and the determination of the achievable SPL from a loudspeaker. Even sophisticated room modeling programs often report SPL incorrectly because of the way that loudspeaker power ratings are measured and entered.

Power Test

I should first clarify the term “power test.” While the term itself is technically correct, it reinforces improper thinking with regard to the specification. The test applies an incrementally increasing drive voltage to a loudspeaker to determine the maximum applicable RMS voltage for linear operation. Electrical power flow to, and dissipation in, the loudspeaker is the result. Ironically, the most useful presentation of the result is not a power rating, but a maximum RMS voltage rating which I will call Vrms_max. This rating can be used “as is” on loudspeaker spec sheets or it can be used to calculate a power rating given the rated impedance of the loudspeaker.

A voltage rating that is converted to a power rating using a rated impedance is not a power rating. It is a voltage rating in disguise that appeals to the “power mind set” of the audio world. As with the other components in the signal chain, there is little interest in the actual power transfer in designing and calibrating sound systems.

Every loudspeaker has a Vrms_max for linear operation, beyond which the loudspeaker misbehaves. There can be several causes for this non-linear response and we generally are not concerned with knowing why. The point is, it’s time to stop turning it up.

Heating and loudness are RMS-related parameters, but the amplifier must also be able to pass the peaks in the program material. RMS (thermal) related failures are far more common than excursion (peak) related failures, so amplifier sizing should be based on RMS, with the amplifier over-sized by a reasonable amount to provide sufficient “peak room” for the signal (determined by the signal’s crest factor).

Voltage Awareness

The system designer must be able to determine the maximum SPL of a design based on the Vrms_max of the loudspeaker, and what size amplifier to specify. The system technician must know the Vrms_max of the loudspeaker, and how to set the gain structure so that the console meters indicate when it has been reached. This tells the system operator when to quit turning it up. Room modeling programs need accurate sensitivity and Vrms_max data for SPL calculations.

It is important to clarify that most references to “power ratings” are actually referring to Vrms_max, even if the rating is expressed in watts. While the actual power consumed by the loudspeaker can be measured, it is not the quantity of interest in the sensitivity and maximum SPL specifications.

Most amplifiers will run out of voltage swing before they run out of current (and power) when properly loaded, so as with a typical household electrical circuit current need only be considered if it is insufficient to meet the demand presented by the load impedance.

Why?

There are at least four objectives for measuring the thermal limits of loudspeakers and expressing the result as Vrms_max. They include

• 1. Determining the maximum long-term SPL that can be produced without destroying the loudspeaker.
• 2. Determining an appropriate amplifier size that can allow the loudspeaker to reach this level within acceptable distortion limits.
• 3. Providing a gain above the reference sensitivity rating for use in room modeling programs.
• 4. Providing the field tech with a voltage that can be checked in situ with an RMS voltmeter to assure that the loudspeaker is not being driven too hard.

Sensitivity

Loudspeaker power testing is inherently tied to the sensitivity specification. Taken together, a sensitivity rating and a Vrms_max rating can reveal the SPL that a loudspeaker can be expected to deliver in a room. The procedure is that the sensitivity is measured with a known drive voltage that is well within the linear operating range of the device. A Vrms_max test determines how much this drive signal can be increased before the loudspeaker becomes non-linear. The traditional drive signal of 1 watt for sensitivity is problematic because it is based on the rated impedance of the loudspeaker – a number that varies wildly between various loudspeaker types. If loudspeakers were simple resistors then determination of the drive voltage for one watt would be straight-forward using a form of the power equation.

where V is the voltage, W is power in watts, and R is resistance in ohms.

Since loudspeakers are not fixed resistors it is not as simple as using 2.83V for 8 ohms and 2V for 4 ohms. What about 6 ohms? What about a piezo element with a rated impedance of 2kΩ? What about a 20 ohm line array box? Who determines the rated impedance? What if we come up with different values? What about two loudspeakers with the same minimum impedance (from which the rated impedance is determined) but different average impedances?

A modern constant voltage amplifier will produce exactly the same voltage into all of these loads, so a voltage-based sensitivity becomes attractive and defendable. A commonly-used value is 2.83Vrms, which would produce 1 watt continuous into an 8 ohm resistor.

Furthermore, the power flow to a loudspeaker is a by-product of the voltage applied to its terminals and its impedance. Power is drawn, not applied. Adjusting the amplifier level modifies the voltage of the waveform, and the amplifier dutifully supplies current relative to the load impedance.

Codependence

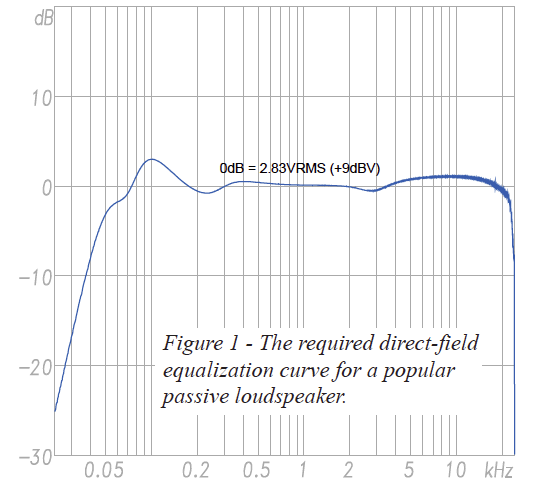
Loudspeaker sensitivity and power ratings are usually seen as unrelated. In fact they are inherently tied together. One reason is that many loudspeakers in the marketplace require active signal processing to produce their reference sensitivity frequency response. The drive signal from a signal processor may vary wildly from 2.83Vrms, possibly only crossing through it at a few frequencies within the bandwidth of the device (see Fig. 1).

So, should 2.83Vrms be the maximum, minimum or average? No Standard exists. This can make a loudspeaker with active equalization appear to have a higher (or lower) sensitivity due to the driving function used. This detail doesn’t matter as long as the same equalization is used for the power test. If the drive voltage for the sensitivity measurement exceeds 2.83Vrms at some frequency, then it will also cause the device to become non-linear sooner as the voltage is increased. What is gained in sensitivity is paid back at the Vrms_max.

A useful way of representing the sensitivity and Vrms_max is as a reference sensitivity accompanied by a gain specification determined from

This tells the investigator:

• 1. The SPL produced by the sensitivity reference signal.
• 2. The additional gain achievable with a larger amplifier before the onset of nonlinearities. This can be calculated from a power rating by 10log(W), where W is the rated power of the loudspeaker found by squaring Vrms_max and dividing by 8 ohms.

Of course, one could add the two metrics to produce the commonly-used “Maximum SPL” but due to the widespread abuse of this spec (the marketing arms race) I prefer to keep them separate. If the claimed SPL seems high (more often than not), it may be apparent whether this is due to an exaggerated sensitivity, Vrms_max or both.

The same method can be used to calculate the maximum SPL from a powered loudspeaker, only in this case the sensitivity reference and Vrms_max will be much lower since we are driving an amplifier input rather than a loudspeaker voice coil.

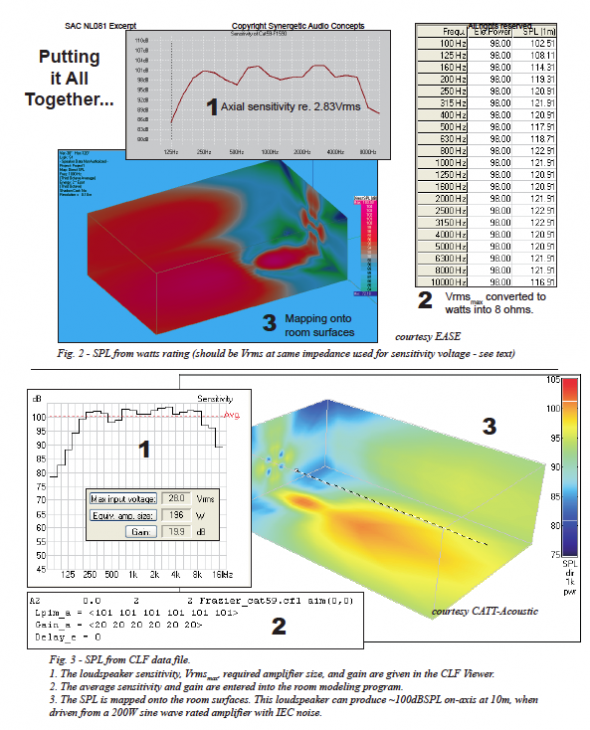
Figures 2 and 3 show the proper way to calculate the maximum SPL in two popular room modeling programs.

A Lower Z Advantage?

One might ask “Doesn’t the use of a fixed voltage give a 4 ohm loudspeaker an advantage over an 8 ohm loudspeaker, since more current will be drawn by the 4 ohm device at a given applied voltage?” It appears to if the sensitivity is taken as stand-alone. The “advantage” goes away when the whole picture is considered, as a less-than-8-ohm loudspeaker presents its own set of problems. Most modern amplifiers have reduced voltage output at 4 ohms than 8 ohms. The 4 ohms device will require a larger gauge cable, and only one should be connected to an amplifier channel. The damping factor will also be lower. It is also likely that the amplifier will be producing more distortion and less bandwidth when loaded to 4 ohms as opposed to 8 ohms.

Clearly any “advantage” of a 4 ohm rated impedance is nullified by these considerations, and it behooves the loudspeaker designer to not let the rated impedance get too low. The fully informed system designer understands the need to look at the whole picture rather than to make judgements based on sensitivity alone.

The End Result

Since the drive voltage for sensitivity uses the voltage derived from the power equation for an 8 ohm loudspeaker (2.83Vrms), then the “power rating” at the thermal limit must make this same assumption. This is not immediately intuitive, because much ado is made about 4 ohm and 2 ohm amplifier ratings and their attendant huge numbers. But think about it – what we are doing is determining the level difference between a starting voltage and a stopping voltage. The formula is

dB = 20log(Vrms_max/V_sens).

The use of impedance is just to provide a means for conversion to watts. If a different impedance is used for the “voltage to power” conversion at the conclusion of the thermal test than was used to determine the voltage used for measuring the sensitivity, then the gain determined by the commonly used 10logW_rated/1W will be incorrect and your room modeling program will report an inaccurate maximum SPL that the loudspeaker can produce. The use of 20log(Vrms_max/V_sens) will report the correct gain for use in the SPL calculation, as will 10log(W_rated/1W) if the same resistance is used for both wattages. Note that in the latter case the resistance just cancels out, leaving the voltage ratio. One could ask “Why bother?”

Abuses of sensitivity and Vrms_max ratings can produce predicted SPLs in room modeling programs that are 10-20dB higher than the device can actually produce.

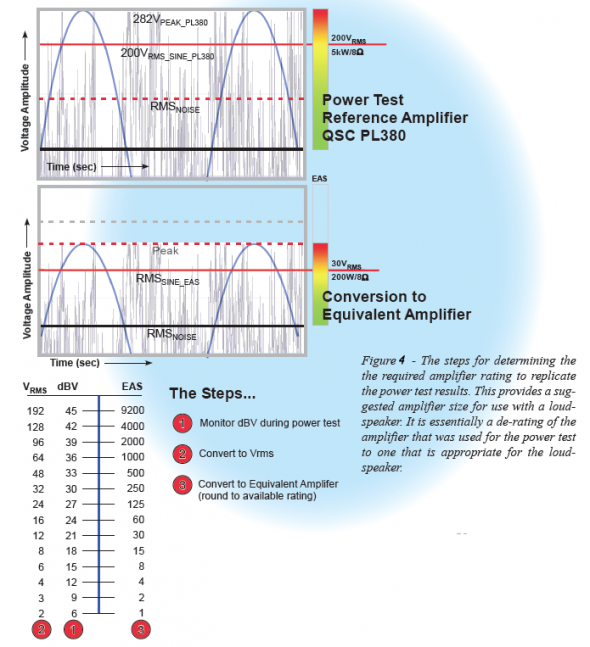
The Equivalent Amplifier Size

There is another useful way of expressing the results of the Vrms_max test. My power test rig uses a QSC PL380 amplifier in the bridged-mono mode of operation. This provides a voltage swing of nearly 300V peak and 200Vrms for a sinusoidal input. This is higher than any single loudspeaker can handle (which is why I use it), and the Vrms_max test always concludes well below the clipping point of the amplifier. Since the sine wave rating of the amplifier is almost always its main power specification, a useful presentation of the test result is to give the sine wave rating for the amplifier required to replicate the test. In other words, “An amplifier with this 8 ohm rating can produce the Vrms_max that the loudspeaker can handle with a 2:1 (6dB) crest factor noise stimulus.” This will make regular speech and music program fall within the thermal capabilities of the loudspeaker, even if the amplifier is driven to clipping. I call this the Equivalent Amplifier Size and it provides a suggested amplifier rating for use with the loudspeaker if the intent is to produce the highest achievable SPL (Figure 4). This frees the designer from having to interpret the loudspeaker power rating for amplifier selection. Equivalently, the EAS is two times the 8 ohm sine wave rating of an amplifier that will pass the voltage waveform at the conclusion of the power test.

There is an option in the CLF to include the EAS.

Conclusion

The metrics needed by sound system designers include a reference sensitivity and a maximum Vrms. These will allow the achievable SPL of the loudspeaker to be determined. Impedance data is needed for amplifier loading and cable selection. For historic reasons, the maximum Vrms is usually expressed as power into a rated impedance. This is fine as long sufficient information is given so that calculating backwards from the power rating produces the correct Vrms_max. In many cases it does not, and the system technician is left with no objective way to determine the maximum drive voltage to the loudspeaker.

These methods have influenced the ratings used in the Common Loudspeaker File format (CLF). pb