Room Modeling Details
This article will answer this question: Room modeling for loudspeaker coverage in high detail takes a lot of time. Is it worth it?
Introduction
In “The Octagon – Part 2” I presented computer-based room models of varying detail and concluded the piece with the decision to proceed with the simple model for executing the design. I got some feedback from readers concerning that choice, their argument being that the detailed model should produce the most accurate simulations of the space. I promised to reinforce my reasoning before proceeding with The Octagon – Part 3. The question becomes “Does a higher detailed model produce a more accurate room impulse response (RIR)?” Of course the answer is “It depends,” so lets have a look at some factors that it depends on.
The Process
To investigate I performed some measured vs. modeled comparisons of a simple, but relevant modeling scenario – the effect of a change in boundary condition for a first order reflection. If higher surface detail results in improved correlation for this carefully controlled exercise, then one could assume that the same would be true for the complete room model. If the boundary behavior evades accurate prediction through precise modeling under well-controlled conditions, then that fact should influence our general approach to modeling entire spaces.
Isolating the Variables
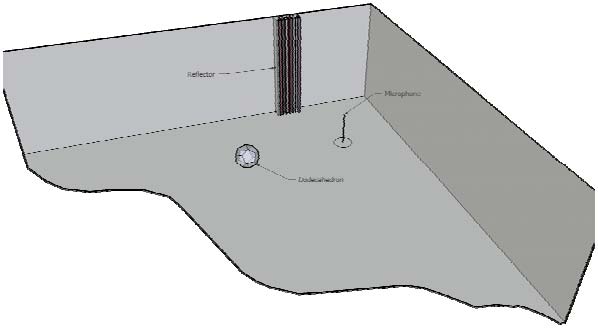
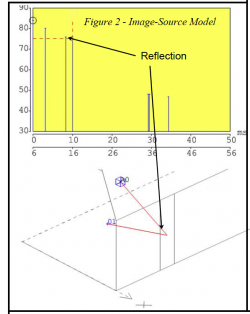
Figure 1 shows the test setup. The “room” consists of three large, reflective room boundaries forming a hard corner. All other room surfaces are highly absorptive and their contributions considered negligible. A spherical sound source (Outline Globe Source™ with 12 transducers) and an omni microphone were placed as indicated. One immediate significant issue is that the Globe Source is not a true omni at high frequencies. This is apparent in the measured data. The IR is not a single spike, but is smeared over time (due to multiple transducers). While not an issue for measuring decay times of auditoriums, it will produce some visual and aural differences between measured and predicted RIRs for this controlled study. The sound source was equalized for flat direct field response at 1-octave resolution, While not necessary for general acoustical measurements, equalization and a relatively flat frequency response magnitude is necessary for comparison to the ideal point source used in the room model. I modeled the space in Sketchup™, and used CATT-Acoustic™ to generate an image source model to identify the first order room reflections (Figure 2). These were physically verified using a large mirror and laser range finder (Figure 1). The left wall first-order reflection will be altered by covering the hard wall with different types of reflectors. I used a stacked pair of RPG diffusors for this purpose, testing both the diffuse side and the smooth side (referred to as “box”), along with the flat wall.
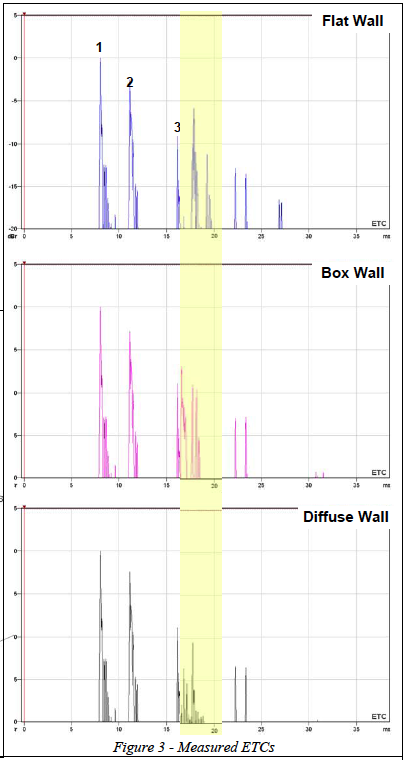
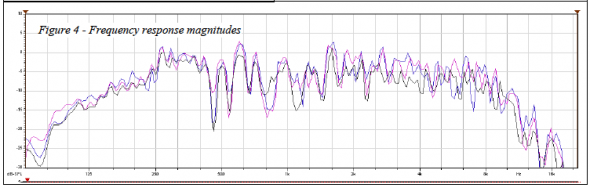
Figure 3 shows the overlaid measured responses on an ETC of sufficient length to include the direct and reflected sound. Room-Capture™ software was used to make the measurements and display the results, due to its very flexible overlay capabilities. The time region effected by changing the surface covering is indicated on the Energy Time Curves (ETC). As can be seen, the direct arrival (1), floor bounce (2), and the other side wall reflection (3) are unaffected by the boundary and present in all RIRs. These early reflections will be integrated by the listener’s ear/brain system and any effects will be perceived in the frequency domain as tonal coloration. Visually they will cause changes to the comb filter pattern of the direct+reflected response (Figure 4).
While the measured change is apparent from the plots, what really matters is the audible change, if any.
This can be evaluated by convolving the IRs with anechoic program material. The IRs are provided for convolution and post-processing. See Project #33 at the SAC IR Exchange.
Use GratisVolver™ to convolve each RIR with speech or music to evaluate the audible difference. Use your favorite measurement program or WAV file editor to view the RIRs. The exercise should be to compare measured with measured and predicted with predicted to evaluate the effect of the boundary change for each.
Predicted Data
I repeated the study in a virtual environment using the room modeling program. RIRs were generated for the same scenarios – flat wall, box and diffusor, plus an additional one for box with scattering coefficient (bottom of this article).
The RPG diffusor was modeled with very high geometrical accuracy, right down to the well-dividers (Figure 5). If detail matters, then this should make it apparent.
CATT-A allows the predicted RIRs to be exported as WAV files, which allows them to be opened in measurement software to facilitate comparison with the measured data. The predicted RIRs are provided for convolution and post-processing in the same file package link above.
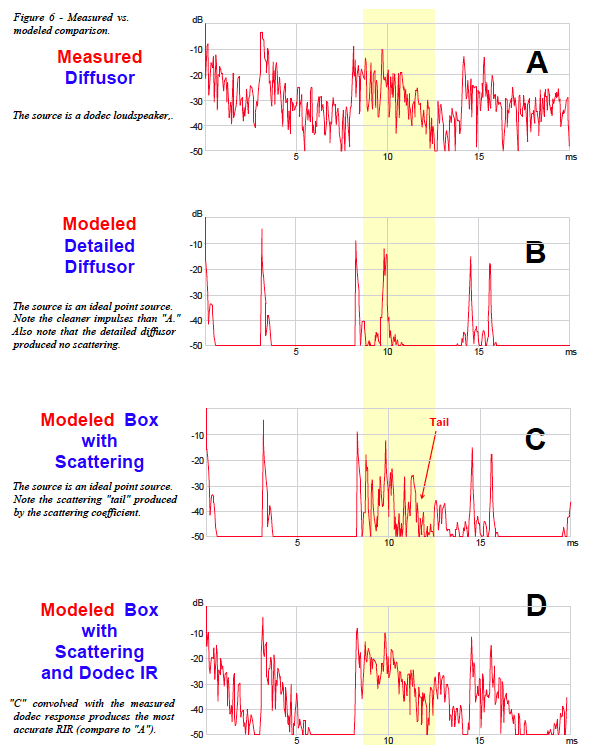
The measured vs. predicted RIRs for the flat wall and box scenarios correlated well and are not presented here. The real interest is in comparing the measured vs. predicted response of the diffusor. These RIRs are presented in Figure 6 as ETCs.
Zoom in and carefully compare the measured diffuse response
(A) with a. the modeled diffuse response
(B), and b. the modeled box response with a surface scattering coefficient applied to the smooth face (C).
It should be pointed out that the smooth surface with scattering would model and measure in a fraction of the time as the detailed model, especially for a full-sized auditorium.
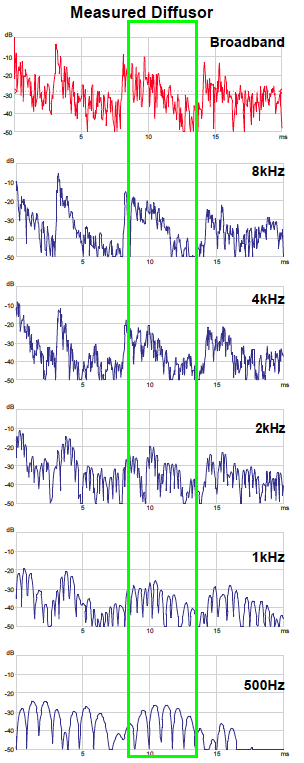
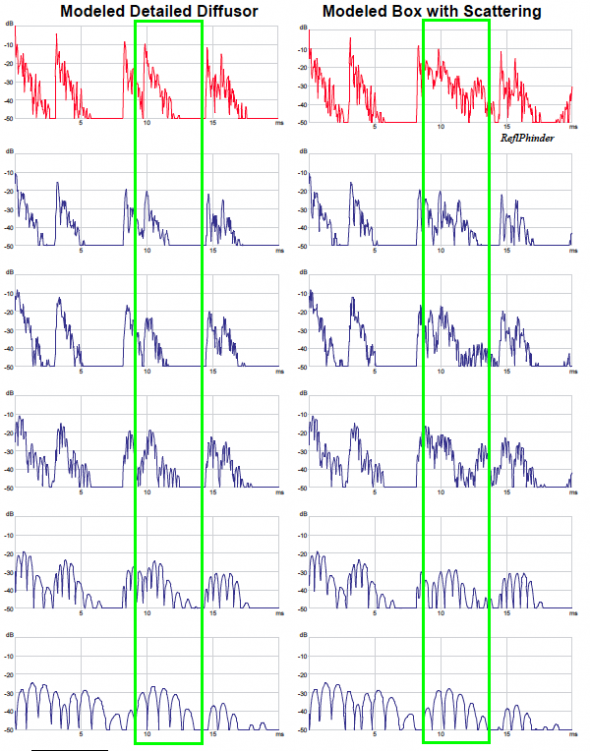
Frequency-Dependence
The real difference between the approaches is in the frequency-dependence of the results. I filtered the measured and predicted RIRs for the diffuse and scattering scenarios in ReflPhinder and provide them in Figure 7. The shaded area highlights the behavior of the diffusor. Note that the smooth box with scattering coefficient better emulates the frequency- dependent behavior of the diffusor, and has the huge advantage in that it is
- – simple to implement
- – faster to calculate
- – can be tweaked per octave band by simply changing the coefficient
Other algorithms for calculating scattering can be used, whereas a high-detail physical model produces one result (unless scattering is used, but then what’s the point of modeling the detail?). Other scattering algos may be examined in future articles.
The “box” model has 15 faces, and the detailed model has 41. Consider the difference for a full-sized auditorium.
Conclusions
I have provided data so that those interested can form their own opinions and draw their own conclusions. I offer mine here.
- – Modeling the diffuse surface exactly failed to reproduce the measured response. This is important. It is not a shortcoming of the modeling program, but a shortcoming of modeling sound as a ray and not including the wave nature of sound.
- – The correlation between measured and predicted time arrivals for first-order reflections was very high. First order reflectors near loudspeakers or listeners in room models should be given careful attention regarding geometry.
- – But, as this study shows the acoustical behavior of complex surfaces can only be approximated. Rather than spend time modeling them in detail, use flat planes with scattering coefficients.
- – If absorption coefficients are only estimates, even more so for scattering coefficients. Don’t worry about being “right,” because you can’t be. Estimates will suffice and an understanding of basic acoustics coupled with experience is the best source of data.
- – The audible difference caused by changing this single reflection in either measurements or predictions is subtle at best. This is another reason to not be concerned with modeling in high detail.
- – The use of flat room planes with frequency-dependent scattering coefficients applied yields an adequate estimate of the behavior of a complex surface, and in this study a superior estimate of the behavior of the diffusor.
- – The floor plane is the most variable of all room surfaces. Its acoustical characteristics will change from event to event, and even during a single event. Even if the seats could be modeled accurately (they can’t) their acoustical behavior would change in the presence of an audience. The use of a boxed-in audience area with appropriate absorption and scattering coefficients is a good general approach, and allows the behavior of the audience plane to be easily tweaked by the investigator.
To Summarize
The use of a frequency-dependent scattering coefficient is one of the most powerful simulation tools available to the sound system designer. When used to randomize complex surfaces, the behavior of specular reflectors that remain in the model can be better observed. A meaningful room model for sound system design work should focus on
- accurate overall room geometry and volume
- estimated absorption and scattering coefficients to produce the proper octave-band reverberation times
- scattering on complex surfaces in lieu of a high degree of modeling details
- accurate loudspeaker data at an appropriate resolution (5deg 1/3-oct in most cases).
A model with these characteristics should suffice for evaluating trade-offs in loudspeaker selection and placement. The subject should be revisited when computer processing power is available to allow the use of advanced approaches to predicting the acoustical behavior of room surfaces, considering the wave nature of sound rather than the use of simple coefficients. Even then, the current methods may prove to be the most practical for the sound system designer. Given the time and money constraints that are present on every project, one should usually use the simplest method that achieves the objective. Less can be more.
Thank you to Bengt-Inge Dalenback for his invaluable input to this study. With these principles established I will proceed with The Octagon – Part 3. pb