More About Square Waves and DC Content
A recent thread on the SAC listserv “Looking for a new DMM” generated a lot of good discussion about transients, clipping, square waves and DC. I thought it might be useful to expound on this a bit. First let’s look at a square wave and see what causes it to have its square shape. A complex waveform can be constructed from, or decomposed into, sine (and cosine) waves of various amplitude and phase relationships. This is the basis of Fourier analysis. A square wave consists of a fundamental sine wave (of the same frequency as the square wave) and odd harmonics of the fundamental. The amplitude of the harmonics is equal to 1/N where N is the harmonic (1, 3, 5, 7…). Each harmonic has the same phase relationship to the fundamental.
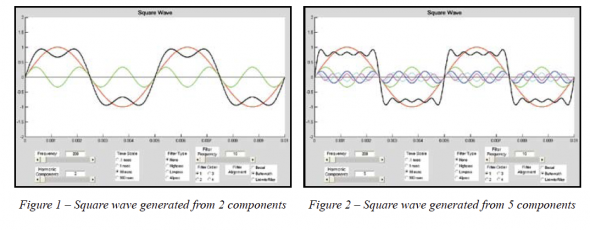
If we construct a square wave from just the first 2 harmonic components we can begin to see how the square shape occurs (Figure 1). We can see here that the red trace is the first harmonic (fundamental) and the green trace is the third harmonic at its correct amplitude. When the first harmonic is at its maximum value the third harmonic is at its minimum value. By adding these two together we get the black trace which is starting to resemble a square wave.
If we now use 5 harmonic components (1, 3, 5, 7 & 9) to construct the square wave we see it really starting to take shape (Figure 2). At the end of each half cycle of the square wave all of the harmonic components are all going the same direction (either positive going or negative going). This is what accounts for the sharp rise. Towards the middle of each half cycle the harmonics alternate between being at minimum and maximum amplitude just as we saw in Figure 1. This is what accounts for the flat portion of the square wave.
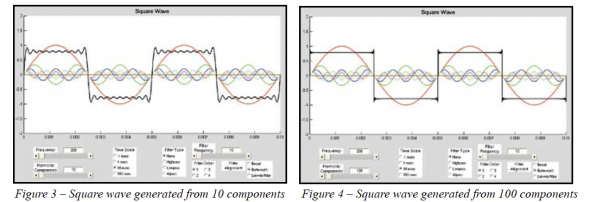
Increasing to 10 harmonic components results in Figure 3. Note that only the first 6 harmonics are shown individually but 10 harmonics are used to generate the square wave.
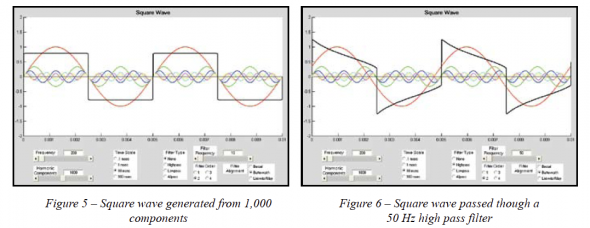
Increasing still further to 100 and 1,000 harmonic components are shown in Figure 4 and Figure 5, respectively. From these graphs it should be well understood that the high frequency harmonic content, and not a DC component (0 Hz), is responsible for the shape of a square wave. In fact, DC by its very definition can not cause any frequency dependent waveform shape. The DC component of a signal is simply the average value of that signal.
Signals that are symmetrical about the time axis will have a DC value of zero. Signals that are asymmetrical about the time axis may or may not have a DC value of zero. If the area between the positive half of the waveform and the time axis is equal to the area between the negative half of the waveform and the time axis there will be no DC component present. If these areas are not equal there will be DC in the signal. In other words, the average value of the signal has to be non-zero if there is DC present in the signal.
To test this for our square wave we will apply a high pass filter below the fundamental of the square wave. Our square wave is at 200 Hz so let’s use a second order (12 dB/octave), 50 Hz high pass filter. The result is shown in Figure 6.
Here we see that the end of each half cycle of the square wave is drooping (or tilting) back towards zero. Some may think this is due to DC being eliminated by the high pass filter. This is not the case. The real reason for the tilt is because of the phase shift of the harmonic components that make up the square wave. Notice that, in the middle of each half cycle, the maximum of the first harmonic (red) is no longer aligned with the maximum/ minimum of the other harmonics. This can also be seen, perhaps more clearly, by looking at the zero crossings. In the previous graphs, whenever the fundamental had a zero crossing all of the other harmonics also had zero crossings. This is not the case in Figure 6 with the high pass filter applied.
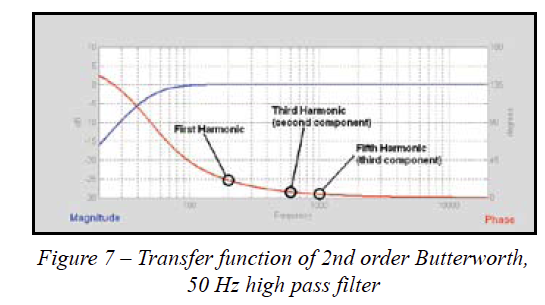
If we look at the response of the 50 Hz high pass filter in the frequency domain (Figure 7) we can see how the phase shift of the harmonic components occur. The phase shift at 200 Hz is approximately 21° relative to the high frequency limit of 0° (no phase shift) which results in the 292 usec time shift of the fundamental. The phase shift of the next component (3rd harmonic, 600 Hz) is approximately 7°. This results in a 32 usec time shift of this component. All of the higher harmonics are subjected to less phase shift (are closer in-phase) and thus occur at roughly the same time. So Figure 7 predicts precisely what we see in Figure 6.
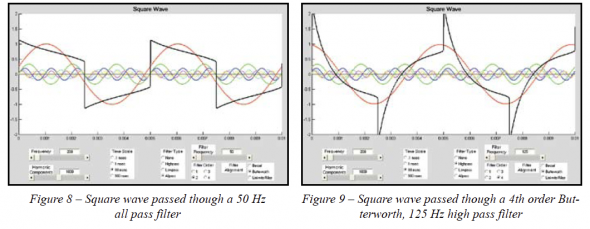
To double check our assertion that the phase response of the 50 Hz high pass filter is the cause of the square wave tilt and not the removal of any DC, let’s pass the square wave through a 50 Hz all pass filter instead of the high pass filter. This will maintain roughly the same phase shift as the high pass filter but the low frequency content of the signal will not be attenuated. If there is any DC component contributing to the square wave we should see a difference (i.e. the tilt should no longer be present). A quick look at Figure 8 should confirm that it is virtually identical to Figure 6 . This should confirm unequivocally that the flat topped structure of a particular waveform is not due to DC. It is instead due to the harmonic content of the signal and the phase relationship of those harmonics to the fundamental.
Hopefully some readers have noticed something interesting about the waveform after it was subjected to an high pass filter (or an all pass filter). The phase shift of the components has caused the peak amplitude at the leading edge of the square wave to increase! The amplitude of the raw square wave (no filtering) is approximately 0.79. After passing through the high pass filter the peak amplitude is approximately 1.25. Increasing the order of the filter or increasing the frequency (up to a limit related to the fundamental of the square wave) will increase the peak amplitude. As seen in Figure 9, with a fourth order Butterworth high pass filter at 125 Hz the peak amplitude exceeds 2.2. This is an increase of the peak amplitude of almost 280% compared to the amplitude of the original square wave!
This highly peaked waveform (no longer a square wave) results when the fundamental and some of the lower harmonics are shifted such that their positive peaks occur at, or very close to, the same time as the positive peaks of the other harmonics. This also occurs for the negative peaks of the fundamental and the negative peaks of the harmonics. Careful inspection of Figure 9 will show this to be the case.
When signals are clipped by devices that do not have sufficient headroom to pass them the tops (and bottoms) of the waveform becomes flattened. Whether the signal is periodic, symmetrical or asymmetrical, the flattening of a waveform (by design or by clipping) can only be accomplished via the addition of in-phase harmonics; just as in the case of a square wave. If the clipping of the signal also results in the area bounded by the waveform above the time axis and below the time axis no longer being equal then a DC component has been introduced into the signal as well. This, however, has no effect on the general shape of the waveform. If the DC component was somehow removed without otherwise affecting the signal, the waveform would simply experience a vertical shift, either up or down, depending on whether the DC component that was removed was greater than or less than zero.
I hope that this has helped to illustrate that it is the harmonic structure (content and phase relationship) of a signal that is responsible for flat-top shaped waveforms. Square waves are merely one example of these types of waveforms.
Thanks to Dale Shirk for off line correspondence during the DMM thread on the listserv and for suggesting this article. ch