Line Array Limitations
Knowing the line array limitations is the key to using them properly.
By Dale ShirkLine array loudspeakers are a popular tool these days. But are they always the best choice? In the interest of preserving Syn-Aud-Con’s slide-rule geek image, let’s examine some of the theoretical limitations of line arrays.
Since a line array can’t be infinitely long, it will have certain limitations. The frequency and distance limits of near field operation are commonly understood. Less well understood are the end effects of a finite line.
The near field can be defined by the following relationship:
where
D is the distance to the far field transition
L is the physical length of the line source
λ = the wavelength of the frequency in question (all lengths in identical units).
Beyond this distance the listener is in the far field and there is 6 dB drop in level per doubling of distance. The transition distance can be quite long at short wavelengths, that is, high frequencies, but it is shorter at low frequencies. For each octave lower in frequency, the transition distance is cut in half.
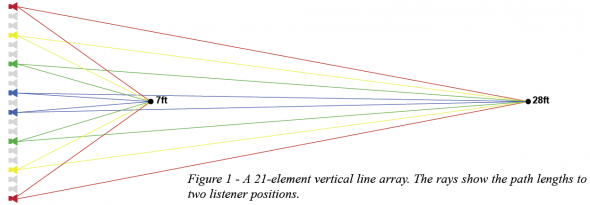
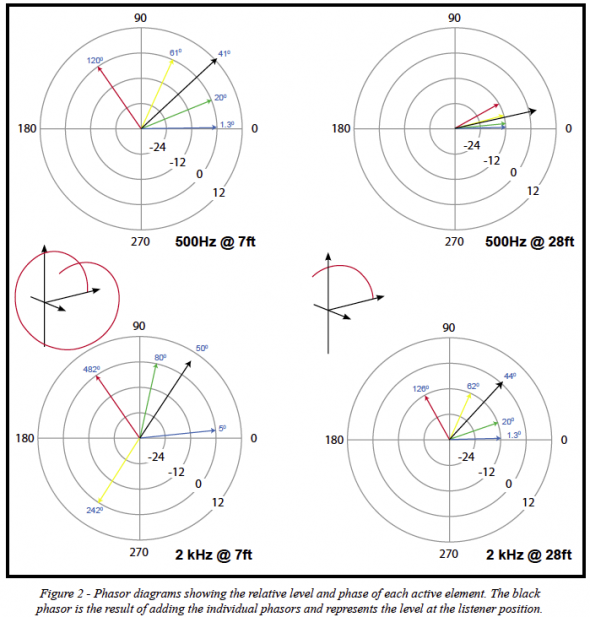
It’s often said that a line array will “throw” high frequencies a long distance, but that’s not quite right. What actually happens is that at close range the high frequencies are lost due to destructive interference. Figure 1 shows a straight, unprocessed 7 foot long line array consisting of 21 drivers with 4-inch (on center) spacing. These are modeled as point sources with no directivity. Four drivers each above and below axis are selected. Their phase is shown relative to the center driver for two frequencies and two distances (Figure 2). The end drivers are farther away and arrive later. The additional phase rotation is the result of their additional time-of-flight. Since the arrivals are not all in phase, they do not sum coherently. The resultant level and phase of all the drivers combined is shown as the black phasor.
At 7 feet away and 500 Hz, the phase of the arrivals fall within a 120 degree window. So they are not all coherently adding together. At 28 ft and 500 Hz, the phase of the arrivals falls within a 32 degree window and are nearly coherent in their summation.
Now look at 7 foot and 2 kHz. Although the same differences in distance are involved, because of the shorter wavelength, the arrivals are scattered over a much wider window of phase. In fact, it is 482 degrees, more than one full rotation. The arrivals on the left side are subtracting signal from the total resulting in destructive interference that reduces high frequency levels for close listeners.
As we move four times farther away, to 28 feet, the arrivals become closer together in phase. Although at the greater overall distance of 28 feet, the arrivals are individually 12dB down, yet because they now sum more coherently, the resultant is only 5dB down. In fact, the near field exists for any frequency and distance where moving farther away will result in more drivers summing coherently, instead of incoherently. Once all drivers sum coherently, the far field is attained.
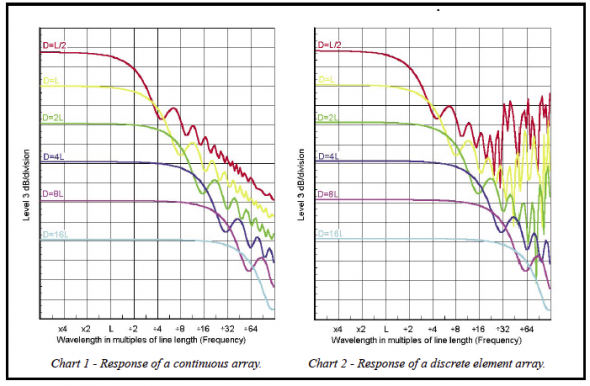
Ponder Chart 1, showing the frequency response vs. distance relative to the line length. This is for a theoretical continuous line, rather than one made up of individual sources. Frequency along the bottom is specified in wavelength relative to line length. For our 7 foot line array, the range shown is 20 – 20kHz. L, the line array length, equals the wavelength of 160Hz, but it could be scaled to other line array lengths as well.
Notice the destructive interference that reduces level at high frequencies. While the 3dB/octave slope needs to be equalized out, you will find, hiding among the ripple, your 3dB-per-doubling-of-distance. Yep, it’s there.
The problem is deciding what distance to perform the equalization. The seats closer or more distant will have frequency response errors. If I equalize at the rear of the room, the front will have a low frequency shelving boost. If I equalize at the front, the rear will have a high frequency shelving boost.
And what about all the ripple? This is for a theoretical continuous line?
Think back for a minute to the phase plots we looked at in Figure 2. Over a range of frequencies, we would be summing arrivals over a half a rotation of phase, then over a full rotation of phase, then a rotation and a half, then two full rotations. The number of arrivals in phase, which add, and the number of arrivals out of phase, which subtract, is constantly changing with frequency. This causes the ripple. It is essentially the same effect we see in FFT measurements when a sample of data is abruptly truncated. In measurements, we apply data window filters to gradually slope the ends of the sample down to zero to reduce these effects.
You might wonder why, when summing phasors from exactly one full rotation of phase, it doesn’t all cancel completely. It’s because there are a greater number of arrivals near zero degrees from the center of the line array than there are near 360 degrees from the end of the line array. This means there are a greater number of arrivals in the first half, 0-180 degrees, than in the second half, 180-360 degrees. Since they are unequal, they don’t completely cancel.
If all this isn’t bad enough, then there’s the added effects of using a finite number of discrete devices. Much has been written about end lobes which occur when the device spacing exceeds one wavelength. But even the on-axis response suffers as the cancellation required to make the near field behave properly doesn’t take place. Chart 2 is the same as Chart 1, only with 21 discrete sources instead of a continuous line. Real world devices with isophasic high frequency sections should behave better than this, as will real world drivers with high frequency directivity.
So far everything we’ve looked at has been on-axis, straight away from the center of the line array. The far field transition takes place at a closer distance when one is off-axis. The physical area where the desirable near field behavior occurs is the full length of the line array when up close, but gets progressively narrower as you move away. It disappears at the furthest transition point on axis. The popular marketing image of a cylindrical wave front shown as a wedge of cheese is not correct. Better to consider it a wedge section of a flying saucer. Instead of staying the full height of the line array to the rear of the room, it narrows vertically to a point.
This has implications for aiming the line array. Sales literature showing the front seat on a line perpendicular to the bottom of the line array, and the rear seat on a line perpendicular to the top of the line array, are simply wrong. This will yield fairly even coverage from the front of the room to the middle, and a strong fall off from the middle to the rear. Instead, as with any other loudspeaker, the strongest output needs to be aimed at the furthest seat.
So what are some practical ways to address these problems? The far field transition that moves with frequency can be addressed by making the line array effectively physically shorter at high frequencies and longer at low frequencies. If the line array length is cut in half for each octave increase in frequency, the transition point will be fixed and the compensation from the equalizer will be valid at all on-axis listeners. Several commercial products use variations of this idea. It can also be done if individual devices are arrayed into a line.
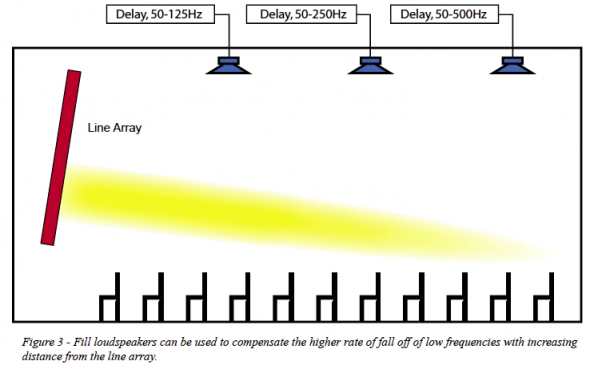
Another way to address this problem of frequency response changing with distance, is to use fill speakers in addition to the line array. The line array is equalized to sound well at the front of the room. Since the low frequencies from the line array are falling off faster towards the rear of the room, than the highs, the fill speakers are processed to fill increasingly higher frequencies as you move towards the rear (Figure 3).
The ripple caused by the abrupt end of the line array can be addressed by reducing the level of the end devices. This becomes the equivalent of the window filtering in an FFT measurement. See Don Keele’s recent AES papers on CBT arrays for more information on this.
Of course, full digital processing on each driver can yield amazing results with line arrays, including reducing many of these problems, as well as steering the output and focusing it to a specific distance and location. While line arrays are not a magic cure-all for every audio problem, they do offer some unique advantages, and when properly applied are a very useful tool. ds